
【题目】在平面直角坐标系中,有三点![]() ,且满足:
,且满足:![]()
(1)求A、B、C三点坐标;
(2)已知,在y轴上有一点![]() ,在坐标轴上是否存在一点P,使△ABP和△ABC的面积相等?若存在,求出P点坐标.若不存在,请说明理由.(C点除外)
,在坐标轴上是否存在一点P,使△ABP和△ABC的面积相等?若存在,求出P点坐标.若不存在,请说明理由.(C点除外)

【答案】(1)![]()
![]()
![]() (2)P(0,5)或P(0,-2)或P(-10,0)
(2)P(0,5)或P(0,-2)或P(-10,0)
【解析】
(1)根据算术平方根的非负性、绝对值的非负性、平方的非负性结合已知条件得出![]() 且
且![]() 且
且![]() ,解出a、b、c的值即可;
,解出a、b、c的值即可;
(2)分①当点P在y轴上时,②当点P在x轴上时两种情况讨论,先求出△ABC的面积,再设出点P的坐标,列出△ABP面积的表达式,进而利用△ABP和△ABC的面积相等得到方程,解方程即可.
解:(1)∵![]() ,且
,且![]() ≥0,
≥0,![]() ≥0,
≥0,![]() ≥0,
≥0,
∴![]() 且
且![]() 且
且![]() ,
,
解得:a=-3,b=3,c=4,
∴A、B、C三点坐标分别为:![]() ,
,![]() ,
,![]() .
.
(2)在坐标轴上存在点P,使△ABP和△ABC的面积相等.理由如下:
如下图1,过点B作BE⊥AC,由第(1)问得:AC=7,BE=3,
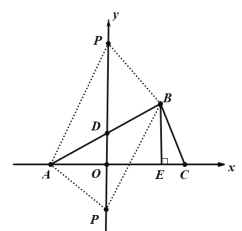
图1
S△ABC=![]() AC·BE=
AC·BE=![]() .
.
①当点P在y轴上时,设点P的坐标为(0,y),
S△ABP=![]() PD·AO+
PD·AO+![]() PD·OE=
PD·OE=![]() PD·(AO+OE) =
PD·(AO+OE) =![]() PD·AE=
PD·AE= ![]() ·|y-
·|y-![]() |×6,
|×6,
∵S△ABP= S△ABC
∴![]() ·|y-
·|y-![]() |×6=
|×6=![]() ,
,
解得:y=5或y=-2,
∴点P的坐标为(0,5)或(0,-2);
②当点P在x轴上时,设点P的坐标为(x,0),如下图2:
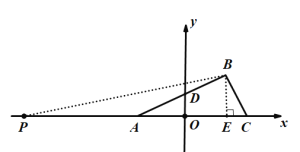
图2
S△ABP=![]() AP·BE=
AP·BE=![]() ·|-3-x|×3,
·|-3-x|×3,
∵S△ABP= S△ABC
∴![]() ·|-3-x|×3=
·|-3-x|×3=![]() ,
,
解得:x=-10或x=4(舍去),
∴点P的坐标为(-10,0).
综上,在坐标轴上存在点P,使△ABP和△ABC的面积相等,点P的坐标为(0,5)或(0,-2)或(-10,0).


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为1,求图中阴影部分的面积(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC,则图中等腰三角形的个数( )
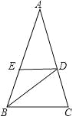
A. 1个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机店卖出甲型号手机10台和乙型号手机12台后的销售额为![]() 万元;卖出甲型号手机6台和乙型号手机9台后的销售额为
万元;卖出甲型号手机6台和乙型号手机9台后的销售额为![]() 万元.
万元.
(1)请问甲型号手机和乙型号手机每台售价为多少元?
(2)若甲型号手机每台进价为1000元,乙型号手机每台进价为800元,预计用不多于![]() 万元且不少于
万元且不少于![]() 万元的资金购进这两种手机共20台,请问有几种进货方案?若所有购进的手机都可以售出,请求出所有方案中的最大利润.
万元的资金购进这两种手机共20台,请问有几种进货方案?若所有购进的手机都可以售出,请求出所有方案中的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形![]() 的底边
的底边![]() 长为
长为![]() ,面积是
,面积是![]() , 腰
, 腰![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 边于
边于![]() 点.若点
点.若点![]() 为
为![]() 边的中点,点
边的中点,点![]() 为线段EF上一动点,则
为线段EF上一动点,则![]() 周长的最小值为( )
周长的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市一座美丽的旅游城市,吸引了很多的外地游客,某旅行社对5月份本社接待的外地游客来郴州旅游的首选景点作了一次抽样调查.调查结果如下图表:(如图)
景点 | 频数 | 频率 |
东江湖 |
|
|
莽山 |
|
|
飞天山 |
| |
苏仙岭 |
|
|
万华岩 |
|
|

![]() 此次共调查了多少人?
此次共调查了多少人?
![]() 请将以上图表补充完整.
请将以上图表补充完整.
![]() 该旅行社预计6月份接待外地来郴的游客
该旅行社预计6月份接待外地来郴的游客![]() 人,请你估计首选去东江湖的人数约有多少人.
人,请你估计首选去东江湖的人数约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动.学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:


请根据图表信息回答下列问题:
(1)频数分布表中的![]() ,
,![]() ;
;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在![]() 小时以上的学生评为“阅读之星”,请你估计该校
小时以上的学生评为“阅读之星”,请你估计该校![]() 名学生中评为“阅读之星”的有多少人?
名学生中评为“阅读之星”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 从原点出发沿数轴向左运动,同时点
从原点出发沿数轴向左运动,同时点![]() 也从原点出发沿数轴向右运动,
也从原点出发沿数轴向右运动,![]() 秒后,两点相距
秒后,两点相距![]() 个单位长度,已知点
个单位长度,已知点![]() 的速度是点
的速度是点![]() 的速度的
的速度的![]() 倍(速度单位:单位长度/秒).
倍(速度单位:单位长度/秒).

(1)求出点![]() 、点
、点![]() 运动的速度,并在数轴上标出
运动的速度,并在数轴上标出![]() ,
,![]() 两点从原点出发运动
两点从原点出发运动![]() 秒时的位置.
秒时的位置.
(2)若![]() ,
,![]() 两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点
两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点![]() 、点
、点![]() 的正中间?
的正中间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com