їјµгЈєФІµДЧЫєПМв,№ґ№Й¶ЁАн,ѕШРОµДЕР¶ЁУлРФЦК,ФІЦЬЅЗ¶ЁАн,ЗРПЯµДРФЦК,ЖЅРРПЯ·ЦПЯ¶ОіЙ±ИАэ,ПаЛЖИэЅЗРОµДЕР¶ЁУлРФЦК,ИсЅЗИэЅЗєЇКэµД¶ЁТе
ЧЁМвЈєЧЫєПМв,·ЦАаМЦВЫ
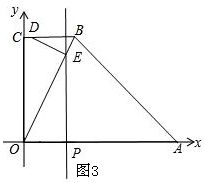
·ЦОцЈєЈЁ1Ј©№эµгBЧчBHЎНOAУЪHЈ¬ИзНј1ЈЁ1Ј©Ј¬ТЧЦ¤ЛД±ЯРОOCBHКЗѕШРОЈ¬ґУ¶шУРOC=BHЈ¬Ц»РиФЪЎчAHBЦРФЛУГИэЅЗєЇКэЗуіцBHјґїЙЈ®
ЈЁ2Ј©№эµгBЧчBHЎНOAУЪHЈ¬№эµгGЧчGFЎНOAУЪFЈ¬№эµгBЧчBRЎНOGУЪRЈ¬Б¬ЅУMNЎўDGЈ¬ИзНј1ЈЁ2Ј©Ј¬ФтУРOH=2Ј¬BH=4Ј¬MNЎНOCЈ®ЙиФІµД°лѕ¶ОЄrЈ¬ФтMN=MB=MD=rЈ®ФЪRtЎчBHDЦРФЛУГ№ґ№Й¶ЁАнїЙЗуіцr=2Ј¬ґУ¶шµГµЅµгDУлµгHЦШєПЈ®ТЧЦ¤ЎчAFGЎЧЎчADBЈ¬ґУ¶шїЙЗуіцAFЎўGFЎўOFЎўOGЎўOBЎўABЎўBGЈ®ЙиOR=xЈ¬АыУГBR2=OB2-OR2=BG2-RG2їЙЗуіцxЈ¬Ѕш¶шїЙЗуіцBRЈ¬ФЪRtЎчORBЦРФЛУГИэЅЗєЇКэѕНїЙЅвѕцОКМвЈ®
ЈЁ3Ј©УЙУЪЎчBDEµДЦ±ЅЗІ»И·¶ЁЈ¬№КРи·ЦЗйїцМЦВЫЈ¬їЙ·ЦИэЦЦЗйїцЈЁўЩЎПBDE=90ЎгЈ¬ўЪЎПBED=90ЎгЈ¬ўЫЎПDBE=90ЎгЈ©МЦВЫЈ¬И»єуФЛУГПаЛЖИэЅЗРОµДРФЦКј°ИэЅЗєЇКэµИЦЄК¶ЅЁБў№ШУЪtµД·ЅіМѕНїЙЅвѕцОКМвЈ®
ЅвґрЈє
ЅвЈєЈЁ1Ј©№эµгBЧчBHЎНOAУЪHЈ¬ИзНј1ЈЁ1Ј©Ј¬
ФтУРЎПBHA=90Ўг=ЎПCOAЈ®
ЎаOCЎОBHЈ®
ЎЯBCЎОOAЈ¬
ЎаЛД±ЯРОOCBHКЗѕШРОЈ®
ЎаOC=BHЈ¬BC=OHЈ®
ЎЯOA=6Ј¬BC=2Ј¬
ЎаAH=0A-OH=OA-BC=6-2=4Ј®
ЎЯЎПBHA=90ЎгЈ¬ЎПBAO=45ЎгЈ¬
ЎаtanЎПBAH=
=1Ј®
ЎаBH=HA=4Ј®
ЎаOC=BH=4Ј®
№Кґр°ёОЄЈє4Ј®
ЈЁ2Ј©№эµгBЧчBHЎНOAУЪHЈ¬№эµгGЧчGFЎНOAУЪFЈ¬№эµгBЧчBRЎНOGУЪRЈ¬
Б¬ЅУMNЎўDGЈ¬ИзНј1ЈЁ2Ј©Ј®
УЙЈЁ1Ј©µГOH=2Ј¬BH=4Ј®
ЎЯOCУлЎСMПаЗРУЪNЈ¬
ЎаMNЎНOCЈ®
ЙиФІµД°лѕ¶ОЄrЈ¬ФтMN=MB=MD=rЈ®
ЎЯBCЎНOCЈ¬OAЎНOCЈ¬
ЎаBCЎОMNЎОOAЈ®
ЎЯBM=DMЈ¬ЎаCN=ONЈ®
ЎаMN=
ЈЁBC+ODЈ©Ј®
ЎаOD=2r-2Ј®
ЎаDH=
=
Ј®
ФЪRtЎчBHDЦРЈ¬
ЎЯЎПBHD=90ЎгЈ¬ЎаBD
2=BH
2+DH
2Ј®
ЎаЈЁ2rЈ©
2=4
2+ЈЁ2r-4Ј©
2Ј®
ЅвµГЈєr=2Ј®

ЎаDH=0Ј¬јґµгDУлµгHЦШєПЈ®
ЎаBDЎН0AЈ¬BD=ADЈ®
ЎЯBDКЗЎСMµДЦ±ѕ¶Ј¬
ЎаЎПBGD=90ЎгЈ¬јґDGЎНABЈ®
ЎаBG=AGЈ®
ЎЯGFЎНOAЈ¬BDЎНOAЈ¬
ЎаGFЎОBDЈ®
ЎаЎчAFGЎЧЎчADBЈ®
Ўа
=
=
=
Ј®
ЎаAF=
AD=2Ј¬GF=
BD=2Ј®
ЎаOF=4Ј®
ЎаOG=
=
=2
Ј®
Н¬АнїЙµГЈєOB=2
Ј¬AB=4
Ј®
ЎаBG=
AB=2
Ј®
ЙиOR=xЈ¬ФтRG=2
-xЈ®
ЎЯBRЎНOGЈ¬
ЎаЎПBRO=ЎПBRG=90ЎгЈ®
ЎаBR
2=OB
2-OR
2=BG
2-RG
2Ј®
ЎаЈЁ2
Ј©
2-x
2=ЈЁ2
Ј©
2-ЈЁ2
-xЈ©
2Ј®
ЅвµГЈєx=
Ј®
ЎаBR
2=OB
2-OR
2=ЈЁ2
Ј©
2-ЈЁ
Ј©
2=
Ј®
ЎаBR=
Ј®
ФЪRtЎчORBЦРЈ¬
sinЎПBOR=
=
=
Ј®
№Кґр°ёОЄЈє
Ј®
ЈЁ3Ј©ўЩµ±ЎПBDE=90ЎгК±Ј¬µгDФЪЦ±ПЯPEЙПЈ¬ИзНј2Ј®
ґЛК±DP=OC=4Ј¬BD+OP=BD+CD=BC=2Ј¬BD=tЈ¬OP=tЈ®

ФтУР2t=2Ј®
ЅвµГЈєt=1Ј®
ФтOP=CD=DB=1Ј®
ЎЯDEЎОOCЈ¬
ЎаЎчBDEЎЧЎчBCOЈ®
Ўа
=
=
Ј®
ЎаDE=2Ј®
ЎаEP=2Ј®
ЎаµгEµДЧш±кОЄЈЁ1Ј¬2Ј©Ј®
ўЪµ±ЎПBED=90ЎгК±Ј¬ИзНј3Ј®
ЎЯЎПDBE=OBCЈ¬ЎПDEB=ЎПBCO=90ЎгЈ¬
ЎаЎчDBEЎЧЎчOBCЈ®
Ўа
=
Ј®
Ўа
=
Ј®
ЎаBE=
tЈ®
ЎЯPEЎОOCЈ¬
ЎаЎПOEP=ЎПBOCЈ®
ЎЯЎПOPE=ЎПBCO=90ЎгЈ¬
ЎаЎчOPEЎЧЎчBCOЈ®
Ўа
=
Ј®
Ўа
=
Ј®
ЎаOE=
tЈ®
ЎЯOE+BE=OB=2
Ј¬
Ўа
t+
t=2
Ј®
ЅвµГЈєt=
Ј®
ЎаOP=
Ј¬OE=
Ј®
ЎаPE=
=
Ј®
ЎаµгEµДЧш±кОЄЈЁ
Ј¬
Ј©Ј®
ўЫµ±ЎПDBE=90ЎгК±Ј¬ИзНј4Ј®
ґЛК±PE=PA=6-tЈ¬OD=OC+BC-t=6-tЈ®
ФтУРOD=PEЈ¬EA=
=
ЈЁ6-tЈ©=6
-
tЈ®

ЎаBE=BA-EA=4
-ЈЁ6
-
tЈ©=
t-2
Ј®
ЎЯPEЎОODЈ¬OD=PEЈ¬ЎПDOP=90ЎгЈ¬
ЎаЛД±ЯРОODEPКЗѕШРОЈ®
ЎаDE=OP=tЈ¬DEЎОOPЈ®
ЎаЎПBED=ЎПBAO=45ЎгЈ®
ФЪRtЎчDBEЦРЈ¬
cosЎПBED=
=
Ј®
ЎаDE=
BEЈ®
Ўаt=
ЈЁ
t-2
Ј©=2t-4Ј®
ЅвµГЈєt=4Ј®
ЎаOP=4Ј¬PE=6-4=2Ј®
ЎаµгEµДЧш±кОЄЈЁ4Ј¬2Ј©Ј®
ЧЫЙПЛщКцЈєµ±ТФBЎўDЎўEОЄ¶ҐµгµДИэЅЗРОКЗЦ±ЅЗИэЅЗРОК±µгEµДЧш±кОЄЈЁ1Ј¬2Ј©ЎўЈЁ
Ј¬
Ј©ЎўЈЁ4Ј¬2Ј©Ј®
µгЖАЈє±ѕМвїјІйБЛФІЦЬЅЗ¶ЁАнЎўЗРПЯµДРФЦКЎўПаЛЖИэЅЗРОµДЕР¶ЁУлРФЦКЎўИэЅЗєЇКэµД¶ЁТеЎўЖЅРРПЯ·ЦПЯ¶ОіЙ±ИАэЎўѕШРОµДЕР¶ЁУлРФЦКЎў№ґ№Й¶ЁАнµИЦЄК¶Ј¬»№їјІйБЛ·ЦАаМЦВЫµДКэС§ЛјПлЈ¬УРТ»¶ЁµДЧЫєПРФЈ®


 ЅвЈєЈЁ1Ј©№эµгBЧчBHЎНOAУЪHЈ¬ИзНј1ЈЁ1Ј©Ј¬
ЅвЈєЈЁ1Ј©№эµгBЧчBHЎНOAУЪHЈ¬ИзНј1ЈЁ1Ј©Ј¬






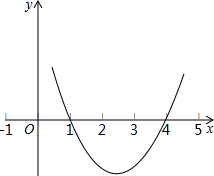 ТСЦЄ¶юґОєЇКэy=ax2-5x+cµДНјПуИзНјЛщКѕЈ®
ТСЦЄ¶юґОєЇКэy=ax2-5x+cµДНјПуИзНјЛщКѕЈ®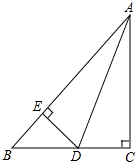 ТСЦЄЈ¬ИзНјЈ¬ADЖЅ·ЦЎПBACЈ¬ЎПC=90ЎгЈ¬DEЎНABЈ¬ДЗГґЈє
ТСЦЄЈ¬ИзНјЈ¬ADЖЅ·ЦЎПBACЈ¬ЎПC=90ЎгЈ¬DEЎНABЈ¬ДЗГґЈє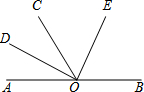 ИзНјЈ¬µгOКЗЦ±ПЯABЙПµДТ»µгЈ¬ЎПAOC=60ЎгЈ¬ODЎўOE·Ц±рКЗЎПAOCЎўЎПBOCµДЅЗЖЅ·ЦПЯЈ®
ИзНјЈ¬µгOКЗЦ±ПЯABЙПµДТ»µгЈ¬ЎПAOC=60ЎгЈ¬ODЎўOE·Ц±рКЗЎПAOCЎўЎПBOCµДЅЗЖЅ·ЦПЯЈ®