练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．如图，某小区规划在一个长80m、宽50m的长方形ABCD上修建三条同样宽的通道，使其中两条与AB平行，另一条与AD平行，其余部分种花草，使花草的种植面积共为3800m2．设通道的宽为xm，可依题意列得方程：（80-2x）（50-x）=3800．

    分析 设通道的宽为xm，将6块草地平移为一个长方形，长为（80-2x）m，宽为（50-x）m．根据长方形面积公式即可列方程（80-2x）（50-x）=3800．

    解答 解：设通道的宽为xm，由题意得：
    （80-2x）（50-x）=3800，
    故答案为（80-2x）（50-x）=3800．

    点评 此题主要考查了由实际问题抽象出一元二次方程，掌握长方形的面积公式，求得6块草地平移为一个长方形的长和宽是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．如图，在平面直角坐标系xOy中，一次函数y=kx+b（k≠0）的图象经过A（0，-2），B（1，0）两点，与反比例函数$y=\frac{m}{x}$（m≠0）的图象在第一象限内交于点M，若△OBM的面积是2．
    （1）求一次函数和反比例函数的表达式；
    （2）若点P是x轴上一点，且满足△AMP是以AM为直角边的直角三角形，请直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知x2-x-2=0，求代数式x（2x-1）-（x+1）（x-1）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．有五张分别印有等边三角形、直角三角形（非等腰）、直角梯形、正方形、圆图形的卡片（卡片中除图案不同外，其余均相同）现将有图案的一面朝下任意摆放，从中任意抽取一张，抽到有轴对称图案的卡片的概率是$\frac{3}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下面计算正确的是（　　）
    A．a+a-1=0B．（$\sqrt{2}$+1）（1-$\sqrt{2}$）=1C．（xy）-1（$\frac{1}{2}$xy）2=$\frac{1}{4}$xyD．-（-a）4÷a2=a2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．先化简，再求值：（x-1-$\frac{8}{x+1}$）÷$\frac{x+3}{x+1}$，并取一个你喜欢的数代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，在坐标系中放置一菱形OABC，已知∠ABC=60°，OA=1．先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2015次，点B的落点依次为B1，B2，B3，…，则B2015的坐标为（1342.5，$\frac{\sqrt{3}}{2}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．先化简，再求值：$\frac{2}{a+1}+\frac{{{a^2}-4a+4}}{{{a^2}-1}}÷\frac{a-2}{a-1}$，其中$a=\sqrt{2}-1$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

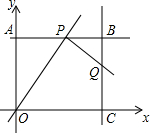    16．如图，在平面直角坐标系中，四边形OABC为矩形，点A、点C分别在y轴、x轴的正半轴上，OA，OC的长分别是方程x2-7x+12=0的两根（OA＜OC）．P为直线AB上一动点，直线PQ⊥OP交直线BC于点Q．
    （1）求点B的坐标；
    （2）当点P在线段AB上运动（不与A，B重合）时，设点P的横坐标为m，线段CQ的长度为l．求出l关于m的函数解析式；
    （3）在坐标平面内是否存在点D，使以O、P、Q、D为顶点的四边形为正方形？若存在，请直接写出D点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案