
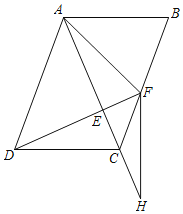
【题目】如图,在平行四边形ABCD中,连接AC,AD=AC,过点D作DF⊥AC交BC于点F,交AC于点E,连接AF.
(1)若AE=4,DE=2EC,求EC的长.
(2)延长AC至点H,连接FH,使∠H=∠EDC,若AB=AF=FH,求证:FD+FC=![]() AD.
AD.
【答案】(1)EC=![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)设EC=x,则DE=2x,AD=AC=AE+EC=4+x,在Rt△ADE中,由勾股定理得出方程,解方程即可;
(2)证明△DEC≌△HEF(AAS),得出EC=EF,DE=EH,得出△CEF是等腰直角三角形,得出∠ECF=45°,再证明△ADE是等腰直角三角形,得出∠DAC=45°,DE=![]() AD,由等腰三角形的性质得出∠ADC=∠ACD=67.5°,求出∠EDC=∠H=22.5°,得出∠CFH=∠EF﹣∠H=22.5°=∠H,证出CF=CH,即可得出结论.
AD,由等腰三角形的性质得出∠ADC=∠ACD=67.5°,求出∠EDC=∠H=22.5°,得出∠CFH=∠EF﹣∠H=22.5°=∠H,证出CF=CH,即可得出结论.
(1)解:设EC=x,则DE=2x,AD=AC=AE+EC=4+x,
∵DF⊥AC,
∴∠AED=90°,
在Rt△ADE中,由勾股定理得:(2x)2+42=(4+x)2,
解得:x=![]() ,或x=0(舍去),
,或x=0(舍去),
∴EC=![]() ;
;
(2)证明:∵四边形ABCD是平行四边形,
∴AB=CD,
∵AB=AF=FH,
∴CD=FH,
∵DF⊥AC,
∴∠DEC=∠HEF=90°,
在△DEC和△HEF中,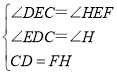 ,
,
∴△DEC≌△HEF(AAS),
∴EC=EF,DE=EH,
∵DF⊥AC,
∴△CEF是等腰直角三角形,
∴∠ECF=45°,
∵AF=FH,DF⊥AC,
∴AE=HE=DE,
∴△ADE是等腰直角三角形,
∴∠DAC=45°,DE=![]() AD,
AD,
∵AD=AC,
∴∠ADC=∠ACD=![]() (180°﹣45°)=67.5°,
(180°﹣45°)=67.5°,
∴∠EDC=∠H=22.5°,
∴∠CFH=∠EF﹣∠H=22.5°=∠H,
∴CF=CH,
∴EF+FC=EC+CH=EH=DE,
∴FD+FC=DE+EF+FC=DE+DE=2DE=![]() AD.
AD.


科目:初中数学 来源: 题型:
【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)写出所有个位数字是5的“两位递增数”;
(2)请用列表法或树状图,求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业,如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,均为300cm,AB的倾斜角为![]() ,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,
,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,![]() 于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30cm,点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少cm(结果保留根号)
于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30cm,点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少cm(结果保留根号)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期伊始,西大附中的学子们积极响应学校的“书香校园”活动,踊跃捐出自己喜爱的书籍,互相分享,让阅读成为一种习惯.据调查,某年级甲班、乙班共80人捐书,丙班有40人捐书,已知乙班人均捐书数量比甲班人均捐书数量多5本,而丙班的人均捐书数量是甲班人均捐书数量的一半,若该年级甲、乙、丙三班的人均捐书数量恰好是乙班人均捐书数量的![]() ,且各班人均捐书数量均为正整数,则甲、乙、丙三班共捐书_____本.
,且各班人均捐书数量均为正整数,则甲、乙、丙三班共捐书_____本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A点坐标为(1,0),C点坐标为(7,0),若点P在直线y=kx+3上运动时,只存在一个点P使∠APC=90°,则k的值是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年广东梅州11分)用如图①,②所示的两个直角三角形(部分边长及角的度数在图中已标出),完成以下两个探究问题:
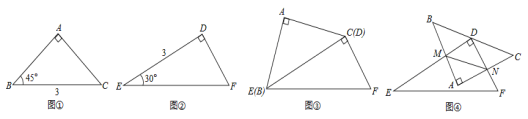
探究一:将以上两个三角形如图③拼接(BC和ED重合),在BC边上有一动点P.
(1)当点P运动到∠CFB的角平分线上时,连接AP,求线段AP的长;
(2)当点P在运动的过程中出现PA=FC时,求∠PAB的度数.
探究二:如图④,将△DEF的顶点D放在△ABC的BC边上的中点处,并以点D为旋转中心旋转△DEF,使△DEF的两直角边与△ABC的两直角边分别交于M、N两点,连接MN.在旋转△DEF的过程中,△AMN的周长是否存在有最小值?若存在,求出它的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
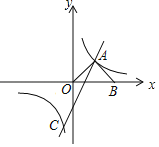
【题目】如图,在平面直角坐标系中,直线y1=2x﹣2与双曲线y2=![]() 交于A、C两点,AB⊥OA交x轴于点B,且OA=AB.
交于A、C两点,AB⊥OA交x轴于点B,且OA=AB.
(1)求双曲线的解析式;
(2)求点C的坐标,并直接写出y1<y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com