
����Ŀ���Ķ����ϣ�С����ѧϰ���θ�ʽ����һЩ�����ŵ�ʽ�ӿ���д����һ��ʽ�ӵ�ƽ������3+![]() =��1+
=��1+![]() ��2������˼����С������������̽����
��2������˼����С������������̽����
��a+b![]() =��m+n
=��m+n![]() ��2������a��b��m��n��������������a+b
��2������a��b��m��n��������������a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ��
��
��a=m2+2n2��b=2mn������С�����ҵ���һ�ְ�����a+b��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
�������С���ķ���̽��������������⣺
��1����a��b��m��n��Ϊ������ʱ����a+b![]() =��m+n
=��m+n![]() )2���ú�m��n��ʽ�ӷֱ��ʾa��b���ã�a=����b=����
)2���ú�m��n��ʽ�ӷֱ��ʾa��b���ã�a=����b=����
��2������̽���Ľ��ۣ���һ��������a��b��m��n ��a��b��������20��
��գ�������+����![]() =��������+������
=��������+������![]() ��2��
��2��
��3����a+6![]() =(m+n
=(m+n![]() )2����a��m��n��Ϊ����������a��ֵ��
)2����a��m��n��Ϊ����������a��ֵ��
���𰸡���1��![]() ����2��8��2��1��1���𰸲�Ψһ������3��12��28.
����2��8��2��1��1���𰸲�Ψһ������3��12��28.
�������������������1��������ȫƽ����ʽ���㷨���ɵó�a��b�ı���ʽ��
��2������ȷ����m��n��������ֵ��Ȼ����ݣ�1���Ľ��ۼ������a��b��ֵ��
��3���������⣬6=2mn������ȷ��m��n��ֵ��ͨ������m=2��n=1����m=1��n=2��Ȼ��ȷ����a��ֵ��
���������(1)��a+b![]() =(m+n
=(m+n![]() )2��
)2��
��a+b![]() =m2+5n2+2mn
=m2+5n2+2mn![]() ��
��
��a=m2+5n2��b=2mn.
�ʴ�Ϊ��m2+5n2��2mn.
(2)��m=1��n=1��
��a= m2+7n2=61��b=2mn=2.
�ʴ�Ϊ8��2��1��1.
(3)�����⣬�ã�
a=m2+3n2��b=2mn��
��6=2mn����m��n��������
��m=3��n=1����m=1��n=3��
��a=32+3��12=12����a=12+3��32=28.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
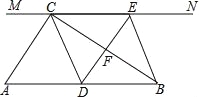
����Ŀ����ͼ����Rt��ABC�У���ACB=90��������C��ֱ��MN��AB��DΪAB����һ�㣬����D��DE��BC����ֱ��MN��E������ΪF������CD��BE��
��1����֤��CE=AD��
��2����D��AB�е�ʱ���ı���BECD��ʲô�����ı��Σ�˵��������ɣ�
��3����DΪAB�е㣬����A�Ĵ�С����ʲô����ʱ���ı���BECD�������Σ���˵��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��m+1��m�C1����x���ϣ����P��������( )
A.��2��0��B.��0��2��C.���C2��0��D.��0���C2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����ABC�У���ACB=90����AC=BC����PCQ=45�����ѡ�PCQ�Ƶ�C��ת����������ת�����У�����A��AD��CP������ΪD��ֱ��AD��CQ��E��
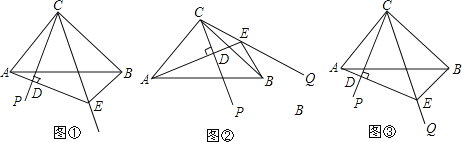
��1����ͼ�٣�����PCQ�ڡ�ACB�ڲ�ʱ����֤��AD+BE=DE��
��2����ͼ��,��CQ�ڡ�ACB�ⲿʱ,��֤AD-BE=DE��
��3���ڣ�1���������£���CD=18��S��BCE=2S��ACD����AE�ij�����ֱ��д�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ţ�1������ѧ��ȤС�龭���г����飬������ij����Ʒ�ڵ�x��1��x��90������ۼ��������������Ϣ���±���
ʱ��x���죩 | 1��x��50 | 50��x��90 |
�ۼۣ�Ԫ/���� | x+40 | 90 |
ÿ������������ | 200��2x | |
��֪����Ʒ�Ľ���Ϊÿ��30Ԫ�������۸���Ʒ��ÿ������ΪyԪ��
��1�����y��x�ĺ�����ϵʽ��
��2�������۸���Ʒ�ڼ���ʱ�������������������������Ƕ��٣�
��3������Ʒ�����۹����У����ж�����ÿ������������4800Ԫ����ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ������ȷ���ǣ�������
A. 2a+b=2ab B. xy��2xy=��1 C. 2x3��x2=x3 D. 4mn��2mn��mn=mn
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��a��b���ڵ�����������M��-ab����a��Ӧ�� ��������
A. ��һ���� B. �ڶ����� C. �������� D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����з���������ͬ��������AA1��BB1��CC1��
��1��С�������������������ѡһ����ǡ��ѡ������AA1�ĸ����Ƕ��٣�
��2��С���ȴ����A��B��C������ͷ�����ѡ������һ���ᣬ�ٴ��Ҷ�A1��B1��C1������ͷ�����ѡ������һ���ᣬ�������������������һ�������ĸ��ʣ�
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com