
 如图,一次函数y=-
如图,一次函数y=-| 3 |
| 3 |
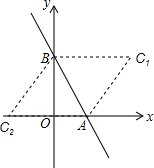 解;(1)∵令y=0,则x=1,令x=0,则y=
解;(1)∵令y=0,则x=1,令x=0,则y=| 3 |
| 3 |
| 3 |
| 3 |
| OB |
| OA |
| 3 |
| 3 |
12+(
|
| 3 |
| 3 |


科目:初中数学 来源: 题型:
 用30m篱笆围成三面是篱笆,一面用墙的矩形菜地.
用30m篱笆围成三面是篱笆,一面用墙的矩形菜地.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、三角形三条中线都能平分三角形的面积 |
| B、三角形三条角平分线交于三角形内一点 |
| C、三角形三条高交于一点 |
| D、三角形的中线、角平分线、高都是线段 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 有一块两条直角边BC、AC的长分别为3厘米和4厘米的Rt△ABC的铁片,现要把它加工成一个面积尽最大的正方形,甲、乙两位师傅加工方案分别如图1和图2所示,请用你学过的知识说明哪位师傅的加工方案符合要求(加工中的损耗忽略不计).
有一块两条直角边BC、AC的长分别为3厘米和4厘米的Rt△ABC的铁片,现要把它加工成一个面积尽最大的正方形,甲、乙两位师傅加工方案分别如图1和图2所示,请用你学过的知识说明哪位师傅的加工方案符合要求(加工中的损耗忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC边于点E.若BE=2,∠B=22.5°
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC边于点E.若BE=2,∠B=22.5°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com