
【题目】已知直线y=x+3交x轴于点A,交y轴于点B,抛物线y=﹣x2+bx+c经过点A,B.
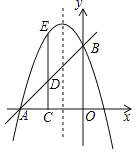
(1)求抛物线解析式;
(2)点C(m,0)在线段OA上(点C不与A,O点重合),CD⊥OA交AB于点D,交抛物线于点E,若DE=![]() AD,求m的值;
AD,求m的值;
(3)点M在抛物线上,点N在抛物线的对称轴上,在(2)的条件下,是否存在以点D,B,M,N为顶点的四边形为平行四边形?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2﹣2x+3;(2)m=﹣2;(3)存在,点N的坐标为(﹣1,﹣2)或(﹣1,0),理由见解析
【解析】
(1)先确定出点A,B坐标,再用待定系数法即可得出结论;
(2)先表示出DE,再利用勾股定理表示出AD,建立方程即可得出结论;
(3)分两种情况:①以BD为一边,判断出△EDB≌△GNM,即可得出结论.
②以BD为对角线,利用中点坐标公式即可得出结论.
(1)当x=0时,y=3,
∴B(0,3),
当y=0时,x+3=0,x=﹣3,
∴A(﹣3,0),
把A(﹣3,0),B(0,3)代入抛物线y=﹣x2+bx+c中得:![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为:y=﹣x2﹣2x+3,
(2)∵CD⊥OA,C(m,0),
∴D(m,m+3),E(m,﹣m2﹣2m+3),
∴DE=(﹣m2﹣2m+3)﹣(m+3)=﹣m2﹣3m,
∵AC=m+3,CD=m+3,
由勾股定理得:AD=![]() (m+3),
(m+3),
∵DE=![]() AD,
AD,
∴﹣m2﹣3m=2(m+3),
∴m1=﹣3(舍),m2=﹣2;
(3)存在,分两种情况:
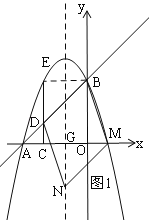
①以BD为一边,如图1,设对称轴与x轴交于点G,
∵C(﹣2,0),
∴D(﹣2,1),E(﹣2,3),
∴E与B关于对称轴对称,
∴BE∥x轴,
∵四边形DNMB是平行四边形,
∴BD=MN,BD∥MN,
∵∠DEB=∠NGM=90°,∠EDB=∠GNM,
∴△EDB≌△GNM,
∴NG=ED=2,
∴N(﹣1,﹣2);
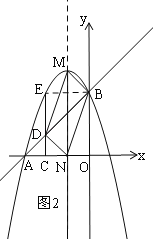
②当BD为对角线时,如图2,
此时四边形BMDN是平行四边形,
设M(n,﹣n2﹣2n+3),N(﹣1,h),
∵B(0,3),D(-2,1),
∴![]()
∴n=-1,h=0
∴N(﹣1,0);
综上所述,点N的坐标为(﹣1,﹣2)或(﹣1,0).


科目:初中数学 来源: 题型:
【题目】某厂家以A、B两种原料,利用不同的工艺手法生产出了甲、乙两种袋装产品,其中,甲产品每袋含1.5千克A原料、1.5千克B原料;乙产品每袋含2千克A原料、1千克B原料.甲、乙两种产品每袋的成本价分别为袋中两种原料的成本价之和.若甲产品每袋售价72元,则利润率为20%.某节庆日,厂家准备生产若干袋甲产品和乙产品,甲产品和乙产品的数量和不超过100袋,会计在核算成本的时候把A原料和B原料的单价看反了,后面发现如果不看反,那么实际成本比核算时的成本少500元,那么厂家在生产甲乙两种产品时实际成本最多为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了奖励优秀班集体,学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元,购买3幅乒乓球拍和2幅羽毛球拍共需204元.
(1)每副乒乓球拍和羽毛球拍的单价各是多少元?
(2)若学校购买5副乒乓球拍和3副羽毛球拍,一共应支出多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
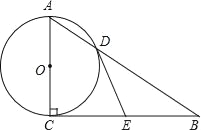
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E.
(1)求证:BE=EC
(2)填空:①若∠B=30°,AC=2![]() ,则DB= ;
,则DB= ;
②当∠B= 度时,以O,D,E,C为顶点的四边形是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
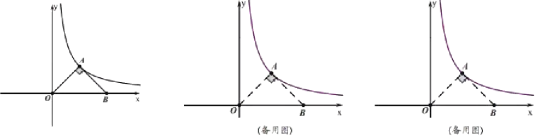
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为原点
为原点![]() 所在直线为
所在直线为![]() 轴建立平面直角坐标系,
轴建立平面直角坐标系,![]() 的顶点
的顶点![]() 在反比例函数
在反比例函数![]() 的图象上.
的图象上.
(1)求反比例函数的解析式:
(2)将![]() 向右平移
向右平移![]() 个单位长度,对应得到
个单位长度,对应得到![]() ,当函数
,当函数![]() 的图象经过
的图象经过![]() 一边的中点时,求
一边的中点时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与x轴交于点A、B,与y轴分别交于点C,其中点
与x轴交于点A、B,与y轴分别交于点C,其中点![]() ,点
,点![]() ,且
,且![]() .
.
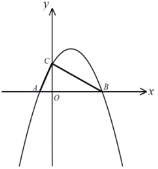
(1)求抛物线的解析式;
(2)点P是线段AB上一动点,过P作![]() 交BC于D,当
交BC于D,当![]() 面积最大时,求点P的坐标;
面积最大时,求点P的坐标;
(3)点M是位于线段BC上方的抛物线上一点,当![]() 恰好等于
恰好等于![]() 中的某个角时,求点M的坐标.
中的某个角时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年“双十一”期间,某快递公司计划租用甲、乙两种车辆快递货物,从货物量来计算:若租用两种车辆合运,10天可以完成任务;若单独租用乙种车辆,完成任务的天数是单独租用甲种车辆完成任务天数的2倍.
(1)求甲、乙两种车辆单独完成任务分别需要多少天?
(2)已知租用甲、乙两种车辆合运需租金65000元,甲种车辆每天的租金比乙种车辆每天的租金多1500元,试问:租甲和乙两种车辆、单独租甲种车辆、单独租乙种车辆这三种租车方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
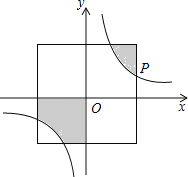
【题目】如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(3a,a)是反比例函数![]() (k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为 ▲ .
(k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为 ▲ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com