
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() 的大小是( )
的大小是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
取DF的中点G,连接AG,根据平行四边形的性质和平行线的性质可得∠FAD=∠AEB=90°,∠CBD=∠GDA,然后根据直角三角形斜边上的中线等于斜边的一半可推出AB=AG=FG=DG,根据等边对等角可得∠ABG=∠AGB,∠GAD=∠GDA,然后根据三角形的外角的性质和已知条件即可求出∠GDA,然后根据直角三角形的两个锐角互余即可得出结论.
解:取DF的中点G,连接AG,如下图所示
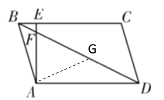
∵四边形ABCD是平行四边形,![]()
∴BC∥AD,∠AEB=90°
∴∠FAD=∠AEB=90°,∠CBD=∠GDA
在Rt△FAD中,DF=2AG=2FG=2GD
∵![]()
∴AB=AG=FG=DG
∴∠ABG=∠AGB,∠GAD=∠GDA
∴∠ABG=∠AGB=∠GAD+∠GDA=2∠GDA=2∠CBD
∴∠ABC=∠ABG+∠CBD=3∠CBD=78°
∴∠CBD=26°
∴∠GDA=26°
在Rt△AFD中,∠AFD=90°-∠GDA=64°
故选B.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】某学校艺术节计划为学生购买A、B两种奖品,已知购买40件A种奖品和购买60件B种奖品共需2600元,购买35件A种奖品和购买70件B种奖品共需2800元.
(1)求A、B两种奖品的单价各为多少元?
(2)若学校购买A、B两种奖品共100件,且购买这批奖品的总费用不超过2800元,求最多购买B奖品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庐阳春风体育运动品商店从厂家购进甲,乙两种T恤共400件,其每件的售价与进货量![]() (件)之间的关系及成本如下表所示:
(件)之间的关系及成本如下表所示:
T恤 | 每件的售价/元 | 每件的成本/元 |
甲 |
| 50 |
乙 |
| 60 |
|
(1)当甲种T恤进货250件时,求两种T恤全部售完的利润是多少元;
(2)若所有的T恤都能售完,求该商店获得的总利润![]() (元)与乙种T恤的进货量
(元)与乙种T恤的进货量![]() (件)之间的函数关系式;
(件)之间的函数关系式;
(3)在(2)的条件下,已知两种T恤进货量都不低于100件,且所进的T恤全部售完,该商店如何安排进货才能使获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张矩形纸片,长15cm,宽9cm,在它的四角各剪去一个同样的小正方形,然折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是48cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为_____.
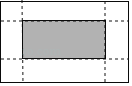
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,经过三角形一顶点和此顶点所对边上的任意一点的直线,均能把三角形分割成两个三角形
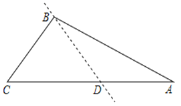
(1)如图,在![]() 中,
中,![]() ,过
,过![]() 作一直线交
作一直线交![]() 于
于![]() ,若
,若![]() 把
把![]() 分割成两个等腰三角形,则
分割成两个等腰三角形,则![]() 的度数是______.
的度数是______.
(2)已知在![]() 中,
中,![]() ,过顶点和顶点对边上一点的直线,把
,过顶点和顶点对边上一点的直线,把![]() 分割成两个等腰三角形,则
分割成两个等腰三角形,则![]() 的最小度数为________.
的最小度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店计划购进一批![]() 、
、![]() 两种型号的计算器,若购进
两种型号的计算器,若购进![]() 型计算器10只和
型计算器10只和![]() 型计算器8只,共需要资金880元;若购进
型计算器8只,共需要资金880元;若购进![]() 型计算器2只和
型计算器2只和![]() 型计算器5只,共需要资金380元.
型计算器5只,共需要资金380元.
(1)求![]() 、
、![]() 两种型号的计算器每只进价各是多少元?
两种型号的计算器每只进价各是多少元?
(2)该商店计划购进这两种型号的计算器共50只.根据市场行情,销售一只![]() 型计算器可获利9元,销售一只
型计算器可获利9元,销售一只![]() 型计算器可获利18元.该商店希望销售完这50只计算器,所获利润不少于购进总成本的25%.则该商店至少要采购
型计算器可获利18元.该商店希望销售完这50只计算器,所获利润不少于购进总成本的25%.则该商店至少要采购![]() 型计算器多少只?
型计算器多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,已知
,已知![]() ,
,![]() .
.

(1)求抛物线的解析式;
(2)如图2,若点![]() 是直线
是直线![]() 上方的抛物线上一动点,过点
上方的抛物线上一动点,过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,当点
,当点![]() 的横坐标为
的横坐标为![]() 时,求
时,求![]() 的面积;
的面积;
(3)若点![]() 为抛物线上的一个动点,以点
为抛物线上的一个动点,以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,当
,当![]() 在运动过程中与直线
在运动过程中与直线![]() 相切时,求点
相切时,求点![]() 的坐标(请直接写出答案).
的坐标(请直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=x+3交x轴于点A,交y轴于点B,抛物线y=﹣x2+bx+c经过点A,B.
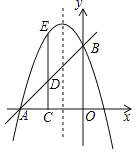
(1)求抛物线解析式;
(2)点C(m,0)在线段OA上(点C不与A,O点重合),CD⊥OA交AB于点D,交抛物线于点E,若DE=![]() AD,求m的值;
AD,求m的值;
(3)点M在抛物线上,点N在抛物线的对称轴上,在(2)的条件下,是否存在以点D,B,M,N为顶点的四边形为平行四边形?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点B(12,10),过点B作x轴的垂线,垂足为A.作y轴的垂线,垂足为C.点D从O出发,沿y轴正方向以每秒1个单位长度运动;点E从O出发,沿x轴正方向以每秒3个单位长度运动;点F从B出发,沿BA方向以每秒2个单位长度运动.当点E运动到点A时,三点随之停止运动,运动过程中△ODE关于直线DE的对称图形是△O′DE,设运动时间为t.
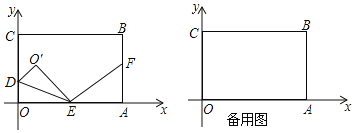
(1)用含t的代数式分别表示点E和点F的坐标;
(2)若△ODE与以点A,E,F为顶点的三角形相似,求t的值;
(3)当t=2时,求O′点在坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com