
【题目】我们知道,经过三角形一顶点和此顶点所对边上的任意一点的直线,均能把三角形分割成两个三角形
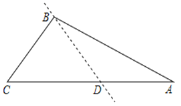
(1)如图,在![]() 中,
中,![]() ,过
,过![]() 作一直线交
作一直线交![]() 于
于![]() ,若
,若![]() 把
把![]() 分割成两个等腰三角形,则
分割成两个等腰三角形,则![]() 的度数是______.
的度数是______.
(2)已知在![]() 中,
中,![]() ,过顶点和顶点对边上一点的直线,把
,过顶点和顶点对边上一点的直线,把![]() 分割成两个等腰三角形,则
分割成两个等腰三角形,则![]() 的最小度数为________.
的最小度数为________.
【答案】![]()
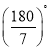
【解析】
(1)由题意得:DA=DB,结合![]() ,即可得到答案;
,即可得到答案;
(2)根据题意,分4种情况讨论,①当BD=AD,CD=AD,②当AD=BD,AC=CD,③AB=AC,当AD=BD=BC,④当AD=BD,CD=BC,分别求出![]() 的度数,即可得到答案.
的度数,即可得到答案.
(1)由题意得:当DA=BA,BD=BA时,不符合题意,
当DA=DB时,则∠ABD=∠A=25°,
∴∠BDA=180°-25°×2=130°.
故答案为:130°;
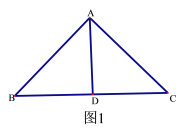
(2)①如图1,∵AB=AC,当BD=AD,CD=AD,
∴∠B=∠C=∠BAD=∠CAD,
∵∠BAC+∠B+∠C=180°,
∴4∠B=180°,
∴∠BAC=90°.
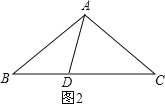
②如图2,∵AB=AC,当AD=BD,AC=CD,
∴∠B=∠C=∠BAD,∠CAD=∠CDA,
∵∠CDA=∠B+∠BAD=2∠B,
∴∠BAC=3∠B,
∵∠BAC+∠B+∠C=180°,
∴5∠B=180°,
∴∠B=36°,
∴∠BAC=108°.
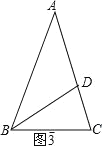
③如图3,∵AB=AC,当AD=BD=BC,
∴∠ABC=∠C,∠BAC=∠ABD,∠BDC=∠C,
∵∠BDC=∠A+∠ABD=2∠BAC,
∴∠ABC=∠C=2∠BAC,
∵∠BAC+∠ABC+∠C=180°,
∴5∠BAC=180°,
∴∠BAC=36°.
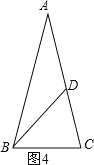
④如图4,∵AB=AC,当AD=BD,CD=BC,
∴∠ABC=∠C,∠BAC=∠ABD,∠CDB=∠CBD,
∵∠BDC=∠BAC+∠ABD=2∠BAC,
∴∠ABC=∠C=3∠BAC,
∵∠BAC+∠ABC+∠C=180°,
∴7∠BAC=180°,
∴∠BAC=![]() .
.
综上所述,∠A的最小度数为:![]() .
.
故答案是:![]() .
.


科目:初中数学 来源: 题型:
【题目】某服装店以每件50元的价格购进![]() 两种服装,已知销售30件
两种服装,已知销售30件![]() 种服装和40件
种服装和40件![]() 种服装共获利润1000元,销售40件
种服装共获利润1000元,销售40件![]() 种服装和50件
种服装和50件![]() 种服装共获利润1300元.
种服装共获利润1300元.
(1)求两种服装每件的售价;
(2)若该服装店准备购进![]() 两种服装共80件,并规定
两种服装共80件,并规定![]() 种服装不少于
种服装不少于![]() 种服装的
种服装的![]() ,设购进
,设购进![]() 种服装
种服装![]() 件,求利润
件,求利润![]() (元)与
(元)与![]() (件)之间的函数解析式,并求出当
(件)之间的函数解析式,并求出当![]() 取何值时,利润最大,最大利润为多少?
取何值时,利润最大,最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD、BC于E、F点,连结CE,若OC![]() cm,CD=4cm,则DE的长为( )
cm,CD=4cm,则DE的长为( )
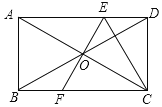
A.![]() cmB.5cmC.3cmD.2cm
cmB.5cmC.3cmD.2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
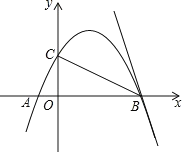
【题目】如图,抛物线y=ax2+bx+2经过点A(1,0),B(4,0),交y轴于点C;
(1)求抛物线的解析式(用一般式表示);
(2)点D为y轴右侧抛物线上一点,是否存在点D使S△ABC=![]() S△ABD?若存在,请求出点D坐标;若不存在,请说明理由;
S△ABD?若存在,请求出点D坐标;若不存在,请说明理由;
(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,
,
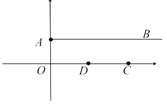
(1)若![]() ,点
,点![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 在射线
在射线![]() 上,当
上,当![]() 是边长为5的等腰三角形,共有几个这样的点
是边长为5的等腰三角形,共有几个这样的点![]() ,并尝试求出点
,并尝试求出点![]() 的坐标;
的坐标;
(2)若直线![]() 与
与![]() 不平行,
不平行,![]() 在直线
在直线![]() 上,是否存在点
上,是否存在点![]() ,使得
,使得![]() 是直角三角形,且
是直角三角形,且![]() ,若存在,求出这样的点
,若存在,求出这样的点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
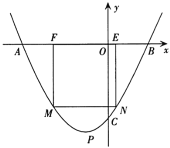
【题目】已知抛物线![]() 的顶点为点
的顶点为点![]() ,与
,与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),与
点的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)直接写出点![]() 的坐标为________;
的坐标为________;
(2)如图,若![]() 、
、![]() 两点在原点的两侧,且
两点在原点的两侧,且![]() ,四边形
,四边形![]() 为正方形,其中顶点
为正方形,其中顶点![]() 、
、![]() 在
在![]() 轴上,
轴上,![]() 、
、![]() 位于抛物线上,求点
位于抛物线上,求点![]() 的坐标;
的坐标;
(3)若线段![]() ,点
,点![]() 为反比例函数
为反比例函数![]() 与抛物线
与抛物线![]() 在第一象限内的交点,设
在第一象限内的交点,设![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC=3,点D在BC上且BD=2CD,E,F分别在AB,AC上运动且始终保持∠EDF=45°,设BE=x,CF=y,则y与x之间的函数关系用图象表示为:( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com