
分析 (1)根据题意m≠0,则计算判别式有△=(2m-1)2≥0,然后根据判别式的意义即可得到结果;
(2)可先用求根公式表示出两根,再根据方程的根都是整数,可求得m的值;
(3)根据一元二次方程的解的定义得到ma2-(2m+1)a+2=0,变形为ma3-(2m+1)a2+2a=0,然后把所求的代数式变形后利用整体代入的方法进行计算.
解答 (1)证明:∵方程mx2-(2m+1)x+2=0是关于x的一元二次方程,
∴m≠0,
∵△=(2m+1)2-4m×2=(2m-1)2≥0,
∴此方程总有两个实数根;
(2)解:x=$\frac{(2m+1)±\sqrt{(2m+1)^{2}-4m×2}}{2m}$,
∴x1=2,x2=$\frac{1}{m}$.
当m为整数1或-1时,x2为整数,即该方程的两个实数根都是整数,
∴m的值为1或-1,
(3)解:∵a是方程的实数根,
∴ma2-(2m+1)a+2=0,
∴ma3-(2m+1)a2+2a=0,
∴ma3=(2m+1)a2-2a代入ma3-(4m+1)a2+4(m+1)a+5得,
∴(2m+1)a2-2a-(4m+1)a2+4(m+1)a+5=-2ma2+(4m+2)a-4+9
=-2[ma2-(2m-1)a+2]+9=9.
点评 本题主要考查一元二次方程根的判别式,掌握一元二次方程根的判别式与一元二次方程根的情况是解题的关键,即△>0?方程有两个不相等的实数根,△=0?方程有两个相等的实数根,△<0?方程无实数根.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
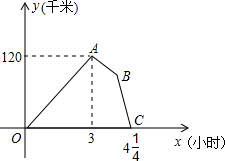 某物流公司的快递车和货车同时从甲地出发,以各自的速度沿平直公路匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:
某物流公司的快递车和货车同时从甲地出发,以各自的速度沿平直公路匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com