
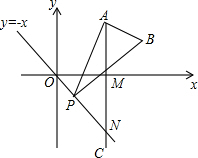
 ��ͼ����֪��A������Ϊ��3��3$\sqrt{3}$����AC��x���ڵ�M����ֱ��y=-x�ڵ�N������P���߶�ON�ϵ�һ�����㣬��APB=30�㣬BA��PA������P�ӵ�O���������߶�ON�����N�˶�ʱ��B��Ҳ��֮�˶���
��ͼ����֪��A������Ϊ��3��3$\sqrt{3}$����AC��x���ڵ�M����ֱ��y=-x�ڵ�N������P���߶�ON�ϵ�һ�����㣬��APB=30�㣬BA��PA������P�ӵ�O���������߶�ON�����N�˶�ʱ��B��Ҳ��֮�˶������� ��1�����ȣ���Ҫ֤���߶�B0Bn���ǵ�B�˶���·������켣�������ͼ����ʾ���������������ο���֤����
��2����Σ����ͼ����ʾ���������������Ρ�AB0Bn�ס�AON������߶�B0Bn�ij��ȣ�����B�˶���·������
��3�����ݴ���ϵ�������ɵú�������ʽ�����ݹ��ɶ������ɵõ��𰸣�
��� �⣺��1����ͼ��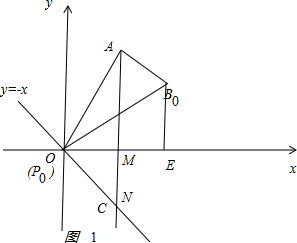 ��
��
AO=$\sqrt{O{M}^{2}+A{M}^{2}}$=6��tan��AOM=$\frac{AM}{OM}$=$\sqrt{3}$��
��AOM=60�㣮
�ߡ�AOB0=30�㣬BA��PA��
��B0O=$\frac{AO}{cos��AO{B}_{0}}$=$\frac{6}{\frac{\sqrt{3}}{2}}$=4$\sqrt{3}$��
���B0OM=30�㣮
OE=B0O•cos30��=4$\sqrt{3}$��B0E=B0O•sin30��=2$\sqrt{3}$��
B0��4$\sqrt{3}$��2$\sqrt{3}$����
��2����ͼ2��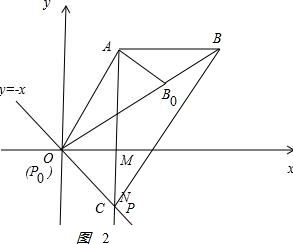 ��
��
�ߡ�OAB0=��PAB=90��
���OAP=��BAB0��
��tan��AOB0=$\frac{A{B}_{0}}{AO}$=$\frac{\sqrt{3}}{3}$��tan��APB=$\frac{AB}{AP}$=$\frac{\sqrt{3}}{3}$��
��$\frac{A{B}_{0}}{AO}$=$\frac{AB}{AP}$��
$\frac{AO}{AP}$=$\frac{A{B}_{0}}{AB}$��
���AOP�ס�AB0B��
��3���ߡ�AOP�ס�AB0B��
��BB0��һ���߶Σ�
��OM=MP=3��
��P��3��-3����AP=3$\sqrt{3}$+3��
AB=AP•tan30��=3+$\sqrt{3}$��
B����6+$\sqrt{3}$��3$\sqrt{3}$����
��BB0�Ľ���ʽΪy=kx+b��
��B��B0��������룬��
$\left\{\begin{array}{l}{��6+\sqrt{3}��k+b=3\sqrt{3}}\\{4\sqrt{3}k+b=2\sqrt{3}}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=\frac{2\sqrt{3}+3}{3}}\\{b=8+4\sqrt{3}}\end{array}\right.$��
BB0�Ľ���ʽΪy=$\frac{2\sqrt{3}+3}{3}$x+8+4$\sqrt{3}$��
BB0=$\sqrt{��6+\sqrt{3}-4\sqrt{3}��^{2}+��3\sqrt{3}-2\sqrt{3}��^{2}}$=$\sqrt{66+36\sqrt{3}}$��
���� ���⿼����һ�κ����ۺ��⣬��1��������������Ǻ����Ķ��壬��2�������˵�ʽ�����ʣ�������Ǻ��������������ε��ж�����3��������������Ǻ���������ϵ������������ʽ�����ɶ�����Ӧ��֪ʶ�϶࣬��Ŀ���ѣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
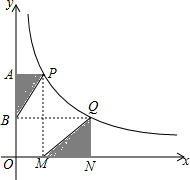 ��ͼ����P��Q�Ƿ���������y=$\frac{k}{x}$��k��0��ͼ���ϵ����㣬PA��y���ڵ�A��QN��x���ڵ�N����PM��x���ڵ�M��QB��y���ڵ�B������PB��QM����S��ABP=S1��S��QMN=S2����S1��S2�Ĵ�С��ϵΪ��������
��ͼ����P��Q�Ƿ���������y=$\frac{k}{x}$��k��0��ͼ���ϵ����㣬PA��y���ڵ�A��QN��x���ڵ�N����PM��x���ڵ�M��QB��y���ڵ�B������PB��QM����S��ABP=S1��S��QMN=S2����S1��S2�Ĵ�С��ϵΪ��������| A�� | S1��S2 | B�� | S1��S2 | C�� | S1=S2 | D�� | ���ж� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
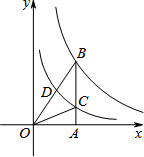 ��ͼ��ʾ����ƽ������ϵ�У�AB��x�ᣬ����������y=$\frac{{k}_{1}}{x}$��k1��0����B�㣬����������y=$\frac{{k}_{2}}{x}$��k2��0����C��D�㣬OC=BC��B��2��3������D�������Ϊ��������
��ͼ��ʾ����ƽ������ϵ�У�AB��x�ᣬ����������y=$\frac{{k}_{1}}{x}$��k1��0����B�㣬����������y=$\frac{{k}_{2}}{x}$��k2��0����C��D�㣬OC=BC��B��2��3������D�������Ϊ��������| A�� | ��$\frac{3}{2}$��$\frac{5}{9}$�� | B�� | ��$\frac{\sqrt{5}}{3}$��$\frac{\sqrt{5}}{2}$�� | C�� | ��$\frac{4}{3}$��$\frac{5}{4}$�� | D�� | ��$\frac{\sqrt{10}}{3}$��$\frac{\sqrt{10}}{2}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
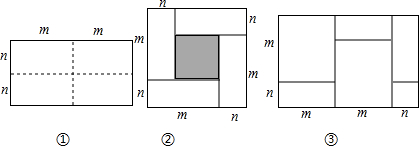
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
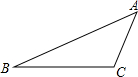 ��ͼ���ڡ�ABC�У���ACB=120�㣬BC=2AC��
��ͼ���ڡ�ABC�У���ACB=120�㣬BC=2AC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
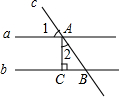 ��ͼ��ֱ��c��ֱ��a��b���ڵ�A��B����a��b���߶�AC��ֱ��ֱ��b������Ϊ��C������1=55�㣬���2�Ķ����ǣ�������
��ͼ��ֱ��c��ֱ��a��b���ڵ�A��B����a��b���߶�AC��ֱ��ֱ��b������Ϊ��C������1=55�㣬���2�Ķ����ǣ�������| A�� | 25�� | B�� | 35�� | C�� | 45�� | D�� | 55�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
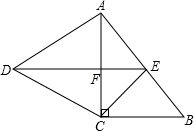 ��ͼ����Rt��ABC�У���ACB=90�㣬��ACΪһ���������ȱ�������ACD����EΪAB���е㣬����DE����AC�ཻ�ڵ�F��
��ͼ����Rt��ABC�У���ACB=90�㣬��ACΪһ���������ȱ�������ACD����EΪAB���е㣬����DE����AC�ཻ�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 16 | B�� | 8 | C�� | 4 | D�� | 2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com