
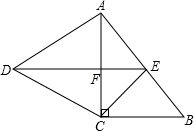
 如图,在Rt△ABC中,∠ACB=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE,与AC相交于点F.
如图,在Rt△ABC中,∠ACB=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE,与AC相交于点F.分析 (1)根据直角三角形的性质和等边三角形的性质得到AE=EC,AD=CD,由全等三角形的判定定理SSS即可证得.
(2)根据菱形的判定定理四条边相等的四边形是菱形证得.
解答 解:(1)∵E是AB中点,∠ACB=90°
∴AE=EC,
∵AD=CD,
在△ADE与△CDE中,
$\left\{\begin{array}{l}{AD=DC}\\{AE=CE}\\{DE=DE}\end{array}\right.$,
∴△ADE≌△CDE;
(2)∵∠B=30°,
∴∠BAC=60°,
∴△ACE是等边三角形,
∴AE=CE=AC,
∵AC=AD=CD,
∴AD=DC=CE=EA,
∴四边形ADCE是菱形.
点评 本题考查了等边三角形的性质,直角三角形的性质,全等三角形的判定与性质,熟记定理是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | y=(x-2)2-3 | B. | y=(x-2)2+3 | C. | y=(x+2)2-3 | D. | y=(x+2)2+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
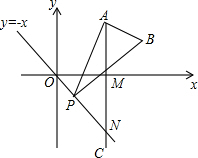 如图,已知点A的坐标为(3,3$\sqrt{3}$),AC⊥x轴于点M,交直线y=-x于点N,若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,若点P从点O出发,在线段ON上向点N运动时,B点也随之运动.
如图,已知点A的坐标为(3,3$\sqrt{3}$),AC⊥x轴于点M,交直线y=-x于点N,若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,若点P从点O出发,在线段ON上向点N运动时,B点也随之运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
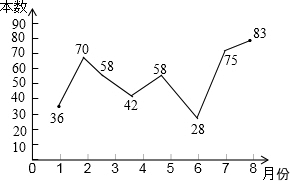 小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )| A. | 阅读数量的平均数是57 | B. | 阅读数量的众数是42 | ||
| C. | 阅读数量的中位数是58 | D. | 有4个月的阅读数量超过60本 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
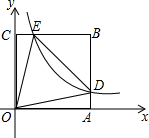 如图,已知反比例函数y=$\frac{k}{x}$(k>0)的图象与正方形OABC的边AB、BC分别交于点D、E.若正方形OABC的边长为1,△ODE是等边三角形,则k的值为2-$\sqrt{3}$.
如图,已知反比例函数y=$\frac{k}{x}$(k>0)的图象与正方形OABC的边AB、BC分别交于点D、E.若正方形OABC的边长为1,△ODE是等边三角形,则k的值为2-$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
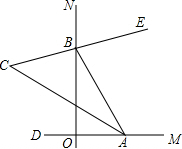 如图,∠MON=90°,点A,B分别在射线OM、ON上移动,BE是∠ABN的平分线,BE的反向延长线与∠OAB平分线相交于点C,试问:∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.
如图,∠MON=90°,点A,B分别在射线OM、ON上移动,BE是∠ABN的平分线,BE的反向延长线与∠OAB平分线相交于点C,试问:∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com