
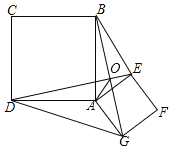
【题目】如图,将小正方形AEFG绕大正方形ABCD的顶点A顺时针旋转一定的角度α(其中0°≤α≤90°),连接BG、DE相交于点O,再连接AO、BE、DG.王凯同学在探究该图形的变化时,提出了四个结论:
①BG=DE;②BG⊥DE;③∠DOA=∠GOA;④S△ADG=S△ABE,其中结论正确的个数有( )
A.1个B.2个C.3个D.4个
【答案】D
【解析】
由“SAS”可证△DAE≌△BAG,可得BG=DE,即可判断①;设点DE与AB交于点P, 由∠ADE=∠ABG,∠DPA=∠BPO,即可判断②;过点A作AM⊥DE,AN⊥BG,易证![]() DE×AM=
DE×AM=![]() ×BG×AN,从而得AM=AN,进而即可判断③;过点G作GH⊥AD,过点E作EQ⊥AD,由“AAS”可证△AEQ≌△GAH,可得AQ=GH,可得S△ADG=S△ABE,即可判断④.
×BG×AN,从而得AM=AN,进而即可判断③;过点G作GH⊥AD,过点E作EQ⊥AD,由“AAS”可证△AEQ≌△GAH,可得AQ=GH,可得S△ADG=S△ABE,即可判断④.
∵∠DAB=∠EAG=90°,
∴∠DAE=∠BAG,
又∵AD=AB,AG=AE,
∴△DAE≌△BAG(SAS),
∴BG=DE,∠ADE=∠ABG,
故①符合题意,
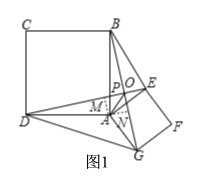
如图1,设点DE与AB交于点P,
∵∠ADE=∠ABG,∠DPA=∠BPO,
∴∠DAP=∠BOP=90°,
∴BG⊥DE,
故②符合题意,
如图1,过点A作AM⊥DE,AN⊥BG,
∵△DAE≌△BAG,
∴S△DAE=S△BAG,
∴![]() DE×AM=
DE×AM=![]() ×BG×AN,
×BG×AN,
又∵DE=BG,
∴AM=AN,且AM⊥DE,AN⊥BG,
∴AO平分∠DOG,
∴∠AOD=∠AOG,
故③符合题意,
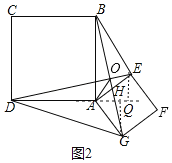
如图2,过点G作GH⊥AD交DA的延长线于点H,过点E作EQ⊥AD交DA的延长线于点Q,
∴∠EAQ+∠AEQ=90°,∠EAQ+∠GAQ=90°,
∴∠AEQ=∠GAQ,
又∵AE=AG,∠EQA=∠AHG=90°,
∴△AEQ≌△GAH(AAS)
∴AQ=GH,
∴![]() AD×GH=
AD×GH=![]() AB×AQ,
AB×AQ,
∴S△ADG=S△ABE,
故④符合题意,
故选:D.


科目:初中数学 来源: 题型:
【题目】小林在使用笔记本电脑时,为了散热,他将电脑放在散热架CAD上,忽略散热架和电脑的厚度,侧面示意图如图1所示,已知电脑显示屏OB与底板OA的夹角为135°,OB=OA=25cm,OE⊥AD于点E,OE=12.5cm.

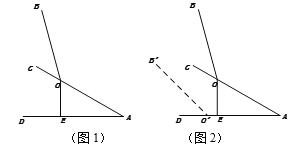
(1)求∠OAE的度数;
(2)若保持显示屏OB与底板OA的135°夹角不变,将电脑平放在桌面上如图2中的![]() 所示,则显示屏顶部
所示,则显示屏顶部![]() 比原来顶部B大约下降了多少?(参考数据:结果精确到0.1cm.参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,
比原来顶部B大约下降了多少?(参考数据:结果精确到0.1cm.参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(﹣2,y2),C(3,y3)都在反比例函数y=![]() (k<0)的图象上,则( )
(k<0)的图象上,则( )
A.y1<y2<y3B.y3<y2<y1C.y3<y1<y2D.y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=
(m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=![]() ,且点B的坐标为(n,﹣2).
,且点B的坐标为(n,﹣2).
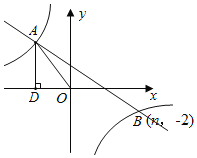
(1)求一次函数与反比例函数的解析式;
(2)请直接写出满足kx+b>![]() 的x的取值范围;
的x的取值范围;
(3)E是y轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴相交于A(﹣1,0),B(m,0)两点,与y轴相交于点C(0,﹣3),抛物线的顶点为D.
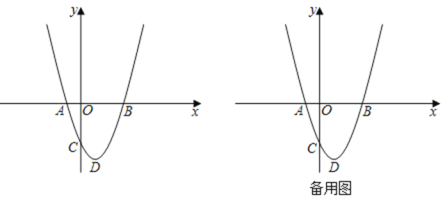
(1)求B、D两点的坐标;
(2)若P是直线BC下方抛物线上任意一点,过点P作PH⊥x轴于点H,与BC交于点M,设F为y轴一动点,当线段PM长度最大时,求PH+HF+![]() CF的最小值;
CF的最小值;
(3)在第(2)问中,当PH+HF+![]() CF取得最小值时,将△OHF绕点O顺时针旋转60°后得到△OH′F′,过点F′作OF′的垂线与x轴交于点Q,点R为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使得点D、Q、R、S为顶点的四边形为菱形,若存在,请直接写出点S的坐标,若不存在,请说明理由.
CF取得最小值时,将△OHF绕点O顺时针旋转60°后得到△OH′F′,过点F′作OF′的垂线与x轴交于点Q,点R为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使得点D、Q、R、S为顶点的四边形为菱形,若存在,请直接写出点S的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.
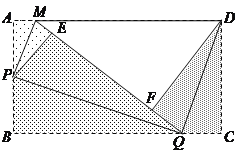
(1)判断△AMP,△BPQ,△CQD和△FDM中有哪几对相似三角形?(不需说明理由)
(2)如果AM=1,sin∠DMF=![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC内接于⊙O,∠BCA=90°,∠CBA=60°,AB=10,点D是AB边上(异于点A,B)的一动点,DE⊥AB交⊙O于点E,交AC于点G,交切线CF于点F.
(1)求证:FC=CG;
(2)①当AE= 时,四辺形BOEC为菱形;
②当AD= 时,OG∥CF.
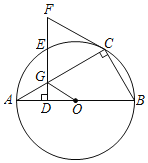
查看答案和解析>>
科目:初中数学 来源: 题型:
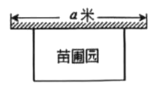
【题目】光明农场准备修建一个矩形苗圃园,苗圃一边靠墙,其他三边用长为48米的篱笆围成.已知墙长为![]() 米.设苗圃园垂直于墙的一边长为
米.设苗圃园垂直于墙的一边长为![]() 米.
米.
(1)求当![]() 为多少米时,苗圃园面积为280平方米;
为多少米时,苗圃园面积为280平方米;
(2)若![]() =22米,当
=22米,当![]() 取何值时,苗圃园的面积最大,并求最大面积.
取何值时,苗圃园的面积最大,并求最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com