
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .设线段
.设线段![]() 的长为
的长为![]() .
.
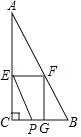
(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
(2)当四边形![]() 为菱形时,求
为菱形时,求![]() 的值.
的值.
(3)设![]() 与矩形
与矩形![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)连结![]() 、
、![]() ,当
,当![]() 与
与![]() 垂直或平行时,直接写出
垂直或平行时,直接写出![]() 的值.
的值.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
![]() ;(4)
;(4)![]() 的值是
的值是![]() 或
或![]() .
.
【解析】
(1)先根据平行线分线段成比例定理可得:![]() ,所以表示CE=2x,AE=4-2x,同理得EF的长,证明四边形CEFG为矩形,可得CG=EF=2-x,分P在G的左侧和右侧分别计算PG的长;
,所以表示CE=2x,AE=4-2x,同理得EF的长,证明四边形CEFG为矩形,可得CG=EF=2-x,分P在G的左侧和右侧分别计算PG的长;
(2)先根据两组对边分别平行可得四边形EPBF是平行四边形,当EF=EP时,列方程解出即可;
(3)先计算当P与G重合时,EF=CP,x=1,分两种情况:
①当0<x≤1时,②当1<x<2时,分别根据三角形面积公式可得结论;
(4)当PF⊥EG时,△PFG∽△EGC,列比例式得方程解出即可;
当PF∥EG时,四边形GEFP是平行四边形,根据EF=GP,列方程解出即可.
解:(1)如图1,
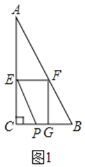
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 为矩形,
为矩形,
∴![]() ,
,
∴![]() ,
,
或![]() ;
;
(2)∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
当![]() 时,即
时,即![]() ,
,
![]() ;
;
(3)当![]() 与
与![]() 重合时,如图2,
重合时,如图2,![]() ,
,
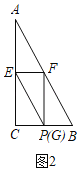
即![]() ,
,
![]() ,
,
分两种情况:
①当![]() 时,如图1,
时,如图1,![]() ;
;
②当![]() 时,如图3,
时,如图3,![]() 交
交![]() 于
于![]() ,
,

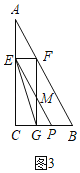
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]() ;
;
(4)当![]() 时,如图4,
时,如图4,
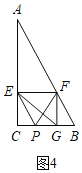
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
当![]() 时,四边形
时,四边形![]() 是平行四边形,
是平行四边形,
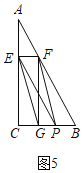
∴![]() ,即
,即![]() ,
,
∴![]() .
.
综上,![]() 的值是
的值是![]() 或
或![]() .
.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:PD=PF;
(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD为台球桌面,AD=240cm,AB=120cm,球目前在G点位置,AG=80cm,如果小丁瞄准BC边上的点F将球打过去,经过点F反弹后碰到CD边上的点H,再经过点H反弹后,球刚好弹到AD边的中点E处落袋.

(1)求证:△BGF∽△DHE;
(2)求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,点A(3,3),点B(4,0),点C(0,-1).
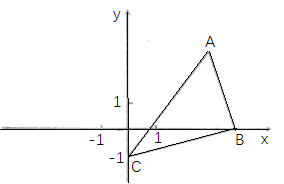
(1)以点C为中心,把△ABC逆时针旋转90°,画出旋转后的图形△A’B’C’(要求尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,
①点A经过的路径AA’的长为________;(结果保留![]() )
)
②写出B’的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为指导某种应季商品的生产和销售,对三月份至七月份该商品的售价和成本进行了调研,结果如下:一件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图甲),一件商品的成本Q(元)与时间t(月)的关系可用一段抛物线上的点来表示,其中6月份成本最高(如图乙).根据图象提供的信息解答下面的问题:
(1)一件商品在3月份出售时的利润是多少元?(利润=售价-成本)
(2)求出一件商品的成本Q(元)与时间t(月)之间的函数关系式;
(3)你能求出3月份至7月份一件商品的利润W(元)与时间t(月)之间的函数关系式吗?若该公司能在一个月内售出此种商品30 000件,请你计算该公司在一个月内最少获利多少元?
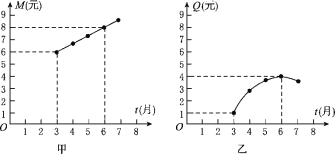
查看答案和解析>>
科目:初中数学 来源: 题型:
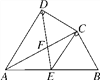
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,连接CE,连接DE交AC于F,AD=4,AB=6.
(1)求证:△ADC∽△ACB;
(2)求AC的值;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
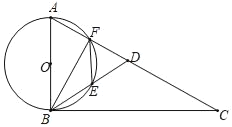
【题目】如图,D为直角△ABC中斜边AC上一点,且AB=AD,以AB为直径的⊙O交AD于点F,交BD于点E,连接BF,BF.
(1)求证:BE=FE;
(2)求证:∠AFE=∠BDC;
(3)已知:sin∠BAE=![]() ,AB=6,求BC的长.
,AB=6,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com