
ЁОЬтФПЁПШчЭМЂйЃЌгаСНИіаЮзДЭъШЋЯрЭЌЕФжБНЧШ§НЧаЮABCКЭEFGЕўЗХдквЛЦ№ЃЈЕуAгыЕуEжиКЯЃЉЃЌвбжЊAC=8cmЃЌBC=6cmЃЌЁЯC=90ЁуЃЌEG=4cmЃЌЁЯEGF=90ЁуЃЌOЪЧЁїEFGаББпЩЯЕФжаЕуЃЎ
ШчЭМЂкЃЌШєећИіЁїEFGДгЭМЂйЕФЮЛжУГіЗЂЃЌвд1cm/sЕФЫйЖШбиЩфЯпABЗНЯђЦНвЦЃЌдкЁїEFGЦНвЦЕФЭЌЪБЃЌЕуPДгЁїEFGЕФЖЅЕуGГіЗЂЃЌвд1cm/sЕФЫйЖШдкжБНЧБпGFЩЯЯђЕуFдЫЖЏЃЌЕБЕуPЕНДяЕуFЪБЃЌЕуPЭЃжЙдЫЖЏЃЌЁїEFGвВЫцжЎЭЃжЙЦНвЦЃЎЩшдЫЖЏЪБМфЮЊxЃЈsЃЉЃЌFGЕФбгГЄЯпНЛACгкHЃЌЫФБпаЮOAHPЕФУцЛ§ЮЊyЃЈcm2ЃЉЃЈВЛПМТЧЕуPгыGЁЂFжиКЯЕФЧщПіЃЉЃЎ
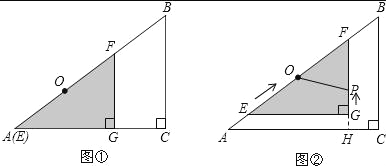
ЃЈ1ЃЉЕБxЮЊКЮжЕЪБЃЌOPЁЮACЃЛ
ЃЈ2ЃЉЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂШЗЖЈздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЪЧЗёДцдкФГвЛЪБПЬЃЌЪЙЫФБпаЮOAHPУцЛ§гыЁїABCУцЛ§ЕФБШЮЊ13ЃК24ЃПШєДцдкЃЌЧѓГіxЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎЃЈВЮПМЪ§ОнЃК1142=12996ЃЌ1152=13225ЃЌ1162=13456Лђ4.42=19.36ЃЌ4.52=20.25ЃЌ4.62=21.16ЃЉ
ЁОД№АИЁПЃЈ1ЃЉx= 1.5sЪБЃЛЃЈ2ЃЉSЫФБпаЮOAHP=![]() x2+
x2+![]() x+3ЃЈ0ЃМxЃМ3ЃЉЃЛЃЈ3ЃЉx=
x+3ЃЈ0ЃМxЃМ3ЃЉЃЛЃЈ3ЃЉx=![]() ЃЈsЃЉЪБ.
ЃЈsЃЉЪБ.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩгкOЪЧEFжаЕуЃЌвђДЫЕБPЮЊFGжаЕуЪБЃЌOPЁЮEGЁЮACЃЌОнДЫПЩЧѓГіxЕФжЕЃЎ
ЃЈ2ЃЉгЩгкЫФБпаЮAHPOаЮзДВЛЙцдђЃЌПЩИљОнШ§НЧаЮAFHКЭШ§НЧаЮOPFЕФУцЛ§ВюРДЕУГіЫФБпаЮAHPOЕФУцЛ§ЃЎШ§НЧаЮAHFжаЃЌAHЕФГЄПЩгУAFЕФГЄКЭЁЯFAHЕФгрЯвжЕЧѓГіЃЌЭЌРэПЩЧѓГіFHЕФБэДяЪНЃЈвВПЩгУЯрЫЦШ§НЧаЮРДЕУГіAHЁЂFHЕФГЄЃЉЃЎШ§НЧаЮOFPжаЃЌПЩЙ§OзїODЁЭFPгкDЃЌPFЕФГЄвзжЊЃЌЖјODЕФГЄЃЌПЩИљОнOFЕФГЄКЭЁЯFODЕФгрЯвжЕЕУГіЃЎгЩДЫПЩЧѓЕУyЁЂxЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ3ЃЉЯШЧѓГіШ§НЧаЮABCКЭЫФБпаЮOAHPЕФУцЛ§ЃЌШЛКѓНЋЦфДњШыЃЈ2ЃЉЕФКЏЪ§ЪНжаМДПЩЕУГіxЕФжЕЃЎ
НтЃКЃЈ1ЃЉЁпRtЁїEFGЁзRtЁїABC
Ёр![]() ЃЌМД
ЃЌМД![]() ,
,
ЁрFG=![]() =3cm
=3cm
ЁпЕБPЮЊFGЕФжаЕуЪБЃЌOPЁЮEGЃЌEGЁЮAC
ЁрOPЁЮAC
Ёрx=![]() =
=![]() ЁС3=1.5ЃЈsЃЉ
ЁС3=1.5ЃЈsЃЉ
ЁрЕБxЮЊ1.5sЪБЃЌOPЁЮACЃЎ
ЃЈ2ЃЉдкRtЁїEFGжаЃЌгЩЙДЙЩЖЈРэЕУEF=5cm
ЁпEGЁЮAH
ЁрЁїEFGЁзЁїAFH
Ёр![]() ,
,
ЁрAH=![]() ЃЈx+5ЃЉЃЌFH=
ЃЈx+5ЃЉЃЌFH=![]() ЃЈx+5ЃЉ
ЃЈx+5ЃЉ
Й§ЕуOзїODЁЭFPЃЌДЙзуЮЊD
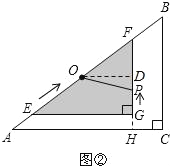
ЁпЕуOЮЊEFжаЕу
ЁрOD=![]() EG=2cm
EG=2cm
ЁпFP=3Љx
ЁрSЫФБпаЮOAHP=SЁїAFHЉSЁїOFP
=![]() AHFHЉ
AHFHЉ![]() ODFP
ODFP
=![]()
![]() ЃЈx+5ЃЉ
ЃЈx+5ЃЉ![]() ЃЈx+5ЃЉЉ
ЃЈx+5ЃЉЉ![]() ЁС2ЁСЃЈ3ЉxЃЉ
ЁС2ЁСЃЈ3ЉxЃЉ
=![]() x2+
x2+![]() x+3ЃЈ0ЃМxЃМ3ЃЉЃЎ
x+3ЃЈ0ЃМxЃМ3ЃЉЃЎ
ЃЈ3ЃЉМйЩшДцдкФГвЛЪБПЬxЃЌЪЙЕУЫФБпаЮOAHPУцЛ§гыЁїABCУцЛ§ЕФБШЮЊ13ЃК24
дђSЫФБпаЮOAHP=![]() ЁСSЁїABC
ЁСSЁїABC
Ёр![]() x2+
x2+![]() x+3=
x+3=![]() ЁС
ЁС![]() ЁС6ЁС8
ЁС6ЁС8
Ёр6x2+85xЉ250=0
НтЕУx1=![]() ЃЌx2=Љ
ЃЌx2=Љ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
Ёп0ЃМxЃМ3
ЁрЕБx=![]() ЃЈsЃЉЪБЃЌЫФБпаЮOAHPУцЛ§гыЁїABCУцЛ§ЕФБШЮЊ13ЃК24ЃЎ
ЃЈsЃЉЪБЃЌЫФБпаЮOAHPУцЛ§гыЁїABCУцЛ§ЕФБШЮЊ13ЃК24ЃЎ


 аТЫМЮЌМйЦкзївЕЪюМйМЊСжДѓбЇГіАцЩчЯЕСаД№АИ
аТЫМЮЌМйЦкзївЕЪюМйМЊСжДѓбЇГіАцЩчЯЕСаД№АИ РЖЬьНЬг§ЪюМйгХЛЏбЇЯАЯЕСаД№АИ
РЖЬьНЬг§ЪюМйгХЛЏбЇЯАЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
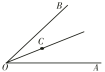
ЁОЬтФПЁПШчЭМЃЌЁЯAOBЃН56ЁуЃЌOCЦНЗжЁЯAOBЃЌШчЙћЩфЯпOAЩЯЕФЕуEТњзуЁїOCEЪЧЕШбќШ§НЧаЮЃЌФЧУДЁЯOECЕФЖШЪ§ЮЊ________________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌЁЯB=90ЁуЃЌABЁЮED ,НЛBCгкEЃЌНЛ ACгкFЃЌ DE = BC,![]() .
.

ЃЈ1ЃЉ ЧѓжЄЃКЁїFCD ЪЧЕШбќШ§НЧаЮ
ЃЈ2ЃЉ ШєAB=3.5cm,ЧѓCDЕФГЄЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпl1ЕФНтЮіЪНЮЊyЃНxЃЌжБЯпl2ЕФНтЮіЪНЮЊyЃНЃ![]() xЃЋ3ЃЌгыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂЕуBЃЌжБЯпl1гыl2НЛгкЕуC.ЕуPЪЧyжсЩЯвЛЕу.
xЃЋ3ЃЌгыxжсЁЂyжсЗжБ№НЛгкЕуAЁЂЕуBЃЌжБЯпl1гыl2НЛгкЕуC.ЕуPЪЧyжсЩЯвЛЕу.
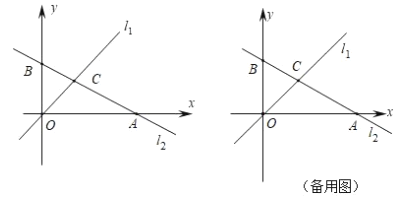
(1)аДГіЯТСаИїЕуЕФзјБъЃКЕуA( ЃЌ )ЁЂЕуB( ЃЌ )ЁЂЕуC( ЃЌ )ЃЛ
(2)ШєSЁїCOPЃНSЁїCOA,ЧыЧѓГіЕуPЕФзјБъЃЛ
(3)ЕБPAЃЋPCзюЖЬЪБЃЌЧѓГіжБЯпPCЕФНтЮіЪН.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ2017еуНЪЁМЮаЫЪаЃЌЕк20ЬтЃЌ8ЗжЃЉШчЭМЃЌвЛДЮКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЉгыЗДБШР§КЏЪ§
ЃЉгыЗДБШР§КЏЪ§![]() ЃЈ
ЃЈ![]() ЃЉЕФЭМЯѓНЛгкЕуAЃЈЉ1ЃЌ2ЃЉЃЌBЃЈmЃЌЉ1ЃЉЃЎ
ЃЉЕФЭМЯѓНЛгкЕуAЃЈЉ1ЃЌ2ЃЉЃЌBЃЈmЃЌЉ1ЃЉЃЎ
ЃЈ1ЃЉЧѓетСНИіКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉдкxжсЩЯЪЧЗёДцдкЕуPЃЈnЃЌ0ЃЉЃЈnЃО0ЃЉЃЌЪЙЁїABPЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓnЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
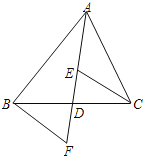
ЁОЬтФПЁПШчЭМЃЌADЪЧЁїABCЕФжаЯпЃЌEЃЌFЗжБ№ЪЧADКЭADбгГЄЯпЩЯЕФЕуЃЌЧвDE=DFЃЌСЌНгBFЃЌCEЃЎЯТСаЫЕЗЈЃКЂйЁїBDFЁеЁїCDEЃЛЂкCE=BFЃЛ ЂлBFЁЮCEЃЛЂмЁїABDКЭЁїACDжмГЄЯрЕШЃЎЦфжае§ШЗЕФга___________ЃЈжЛЬюађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуCЪЧЯпЖЮABЩЯГ§ЕуAЁЂBЭтЕФШЮвтвЛЕуЃЌЗжБ№вдACЁЂBCЮЊБпдкЯпЖЮABЕФЭЌХдзїЕШБпЁїACDКЭЕШБпЁїBCEЃЌСЌНгAEНЛDCгкMЃЌСЌНгBDНЛCEгкNЃЌСЌНгMNЃЎ
ЃЈ1ЃЉЧѓжЄЃКAEЃНBDЃЛ
ЃЈ2ЃЉЧыХаЖЯЁїCMNЕФаЮзДЃЌВЂЫЕУїРэгЩЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
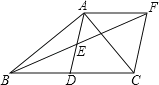
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌADЪЧжаЯпЃЌEЪЧADЕФжаЕуЃЌЙ§ЕуAзїAFЁЮBCНЛBEЕФбгГЄЯпгкЕуFЃЌСЌНгCF
ЃЈ1ЃЉЧѓжЄЃКADЃНCFЃЛ
ЃЈ2ЃЉШчЙћABЃНACЃЌЫФБпаЮADCFЕФаЮзДЮЊЁЁ ЁЁЃЈжБНгаДГіНсЙћЃЉЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
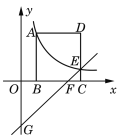
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФЖЅЕуBЃЌCдкxжсЕФе§АыжсЩЯЃЌЗДБШР§КЏЪ§yЃН![]() (kЁй0)дкЕквЛЯѓЯоЕФЭМЯѓОЙ§ЖЅЕуA(mЃЌ2)КЭCDБпЩЯЕФЕуE(nЃЌ
(kЁй0)дкЕквЛЯѓЯоЕФЭМЯѓОЙ§ЖЅЕуA(mЃЌ2)КЭCDБпЩЯЕФЕуE(nЃЌ![]() )ЃЌЙ§ЕуEЕФжБЯпlНЛxжсгкЕуFЃЌНЛyжсгкЕуG(0ЃЌЃ2)ЃЌдђЕуFЕФзјБъЪЧ(ЁЁЁЁ)
)ЃЌЙ§ЕуEЕФжБЯпlНЛxжсгкЕуFЃЌНЛyжсгкЕуG(0ЃЌЃ2)ЃЌдђЕуFЕФзјБъЪЧ(ЁЁЁЁ)
A. (![]() ЃЌ0)B. (
ЃЌ0)B. (![]() ЃЌ0)C. (
ЃЌ0)C. (![]() ЃЌ0)D. (
ЃЌ0)D. (![]() ЃЌ0)
ЃЌ0)
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com