
����Ŀ����ͼ1��Rt��ABC�У���D��E�ֱ�Ϊֱ�DZ�AC��BC�ϵĵ㣬������AD2+BE2��DE2�����DEΪR��ABC���������ָ���������Ȼ����DEΪ��ABC����λ��ʱ��DE�ǡ�ABC��һ�������ָ��ߣ�
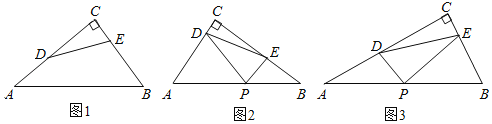
��1����ͼ1��AB��10��cosA��![]() ��AD��3����DEΪ�����ָ��ߣ���BE�ij����� ����
��AD��3����DEΪ�����ָ��ߣ���BE�ij����� ����
��2����ͼ2����AC���ϵĵ�D����Rt��ABC�е�б��AB��ȡ��P��ʹ��DP��DA������P��PE��PD��BC�ڵ�E������DE����֤��DE��ֱ�ǡ�ABC�������ָ��ߣ�
��3����ͼ3����Rt��ABC�У�AC��10��BC��5��DE���������ָ��ߣ���P��б��AB���е㣬����PD��PE����cos��PDE��ֵ��
���𰸡���1��![]() ����2�������������3��
����2�������������3��![]()
��������
��1�������������BC�ij�����BE��x����CE��6��x���ɹ��ɶ�����DE2��CD2+CE2��52+��6��x��2�����뵽AD2+BE2��DE2�м������BE��
��2���ָ��������ҳ�EP=EB�����ɹ��ɶ����ó�DP2+EP2��DE2=AD2+BE2��DE��ֱ�ǡ�ABC�������ָ��ߣ�
��3���������������ߣ��ӳ�DP��F��ʹPF��PD������BF��EF����������ó�ED��EF��
�ٹ���P��PM��AC��PN��BC��֤����MPD�ס�NPE����PD��a����PE��2a�����DE���������cos��PDE��ֵ��
�⣺��1����AB��10��cosA��![]() ��
��
��cosA��![]() ��
��
��AC��8��CD��5��
��BC=![]() ��
��![]() ��6��
��6��
��BE��x����CE��6��x��
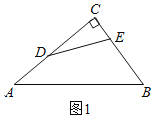
��Rt��CDE��DE2��CD2+CE2��52+��6��x��2��
��DEΪ�����ָ��ߣ�
��AD2+BE2��DE2��
��32+x2��52+��6��x��2��
��ã�x��![]() ��
��
��BE��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2��֤������ͼ2��

��DA��DP��
���DAP����DPA��
��PE��PD��
���DPA+��EPB��90����
�֡�A����B��
���EPB����B��
��EP��EB��
��AD2+BE2��DP2+EP2��DE2��
��DE��ֱ�ǡ�ABC�������ָ��ߣ�
��3���⣺�ӳ�DP��F��ʹPF��PD������BF��EF��
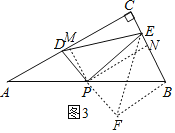
��AP��BP����APD����BPF��
���APD�ա�BPF��SAS����
��AD��BF����A����FBP��
���EBF����CBA+��FBP����CBA+��A��90����
��DE�������ָ��ߣ�
��DE2��AD2+BE2��BF2+BE2��EF2����ED��EF��
��PD��PF��
���EPD��90����
����P��PM��AC��PN��BC��
���MPD����NPE��90������MPE��
���MPD�ס�NPE��
��![]() ��
��
��PD��a����PE��2a����DE��![]() ��
��![]() a��
a��
��cos��PDE��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �ı�
�ı�![]() ��������
��������![]() �ı�
�ı�![]() �ϣ�����
�ϣ�����![]() ��
��![]() ��
��
��1���۲����![]() ��
��![]() ֮��Ĵ�С��ϵ����֤����Ľ��ۣ�
֮��Ĵ�С��ϵ����֤����Ľ��ۣ�
��2��ͼ���Ƿ����ͨ����ת�ܹ������غϵ����������Σ������ڣ�˵����ת���̣��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��"�һ���ˮ��Ȼȥ��������ط��˼�."�һ�����2017�����¹��Ӵ��ο�![]() ���ˣ�2018�����±�2017������������������5%����֪2017��������2019�����������һ����ο�����ƽ����������Ϊ8%����2019�����±�2018�������ο���������
���ˣ�2018�����±�2017������������������5%����֪2017��������2019�����������һ����ο�����ƽ����������Ϊ8%����2019�����±�2018�������ο���������![]() ������з���Ϊ( )
������з���Ϊ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
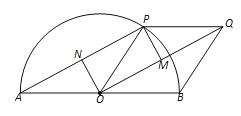
����Ŀ����ͼ����֪ABΪ��ԲO��ֱ����PΪ��Բ�ϵ�һ�����㣨�����˵㣩����OP��OBΪһ���ڱ���POBQ������OQ��AP����OQ��AP���е�ֱ�ΪM��N������PM��ON��
��1�����ж��ı���OMPN����״����˵�����ɣ�
��2������P�ӵ�B��������ÿ��15�����ٶȣ��Ƶ�O�ڰ�Բ����ʱ�뷽���˶������˶�ʱ��Ϊts��
������tΪ��ֵʱ���ı���OMPN�����ȡ�����ֵ�����жϴ�ʱֱ��PQ���ԲO��λ�ù�ϵ����˵�����ɣ���
���Ƿ����������t��ʹ�õ�Q���ڰ�ԲO�ڣ������ڣ���ֱ��д��t��ȡֵ��Χ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
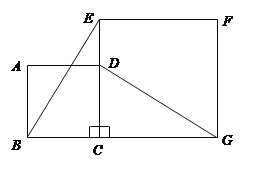
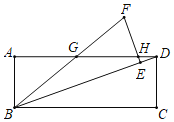
����Ŀ����ͼ������ABCD�У�����BCD�Ƶ�B��ʱ����ת�á�BEF�����е�C�Ķ�Ӧ��Eǡ������BD�ϣ�BF��EF�ֱ�AD�ڵ�G��H����GH��4HD����cos��DBC��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
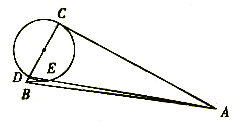
����Ŀ����Rt��ABC�У���ACB=90��.AC=8��BC=3����D��BC���϶��㣬����AD����CDΪֱ����Բ�ڵ�E�����߶�BE���ȵ���СֵΪ( )
A.1B.![]() C.
C. ![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() ��һ��
��һ��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
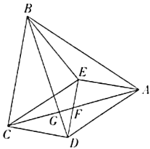
��1��![]() �Ķ���Ϊ__________��
�Ķ���Ϊ__________��
��2�����ı���![]() ��ƽ���ı���
��ƽ���ı���
����֤��![]() ��
��
����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
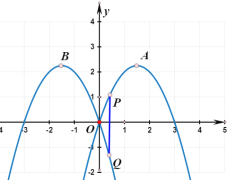
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ����������
����������![]() ��
��![]() �ᷭ�۵õ�������
�ᷭ�۵õ�������![]() ��������
��������![]() ��
��![]() �Ķ���ֱ�Ϊ
�Ķ���ֱ�Ϊ![]() ��
��![]() ����
����![]() ������
Ϊ������![]() ��һ�㣬������Ϊ
��һ�㣬������Ϊ![]() ������
������![]() ��
��![]() ���ƽ���߽�������
���ƽ���߽�������![]() �ڵ�
�ڵ�![]() ��
��
��1����![]() ʱ��
ʱ��
����ֱ��д��������![]() �Ľ���ʽ��
�Ľ���ʽ��
�ڵ�![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
��2����![]() ʱ��
ʱ��
��![]() ������
Ϊ������![]() ��һ���㣬��
��һ���㣬��![]() Ϊ����ֱ��������ʱ����
Ϊ����ֱ��������ʱ����![]() ��ֵ��
��ֵ��
����![]() ��������������
Ϊ��������������![]() ���������Ϊ�����ĵ��Ϊ������㡱����������
���������Ϊ�����ĵ��Ϊ������㡱����������![]() ���ڲ������������ϣ���6��������㡱ʱ��ֱ��д��
���ڲ������������ϣ���6��������㡱ʱ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
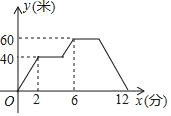
����Ŀ��С������ϰ�ٿغ������˻������ͺ����˻�������������ʱ���ٶ���ͬ�������˻��ķ��и߶�Ϊy���ף���С���ٿ����˷ɻ���ʱ��Ϊx���֣���y��x֮��ĺ���ͼ����ͼ��ʾ��
��1�����˻��������ٶ�Ϊ�� ����/�֣����˻���40�ĸ߶��Ϸ������� ���֣�
��2�������˻���������У�y��x֮��ĺ�����ϵʽ��
��3�������˻������ĸ߶�Ϊ50��ʱx��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com