
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,与y轴相交于点C,直线y=kx+n(k≠0)经过B,C两点,已知A(1,0),C(0,3),且BC=5.
(1)分别求直线BC和抛物线的解析式(关系式);
(2)在抛物线的对称轴上是否存在点P,使得以B,C,P三点为顶点的三角形是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.

【答案】(1)直线BC的解析式为y=﹣![]() x+3;抛物线解析式为y=
x+3;抛物线解析式为y=![]() x2﹣
x2﹣![]() x+3;(2)存在.P1(
x+3;(2)存在.P1(![]() ,
,![]() ),P2(
),P2(![]() ,﹣2),P3(
,﹣2),P3(![]() ,
,![]() ),P4(
),P4(![]() ,
,![]() ).
).
【解析】
试题分析:(1)由C的坐标确定出OC的长,在直角三角形BOC中,利用勾股定理求出OB的长,确定出点B坐标,把B与C坐标代入直线解析式求出k与n的值,确定出直线BC解析式,把A与B坐标代入抛物线解析式求出a的值,确定出抛物线解析式即可;(2)在抛物线的对称轴上存在点P,使得以B,C,P三点为顶点的三角形是直角三角形,如图所示,分三种情况考虑:当PC⊥CB时,△PBC为直角三角形;当P′B⊥BC时,△BCP′为直角三角形,当点P为直角顶点,即PC⊥PB时,△PBC为直角三角形;分别求出P的坐标即可.
试题解析:(1)由C的坐标确定出OC的长,∵C(0,3),即OC=3,∵BC=5,∴在Rt△BOC中,根据勾股定理得:OB=![]() =4,即B(4,0),把B与C坐标代入y=kx+n中,得:
=4,即B(4,0),把B与C坐标代入y=kx+n中,得:![]() ,解得:k=﹣
,解得:k=﹣![]() ,n=3,∴直线BC的解析式为y=﹣
,n=3,∴直线BC的解析式为y=﹣![]() x+3;由A(1,0),B(4,0),设抛物线解析式为y=a(x﹣1)(x﹣4)=ax2﹣5ax+4a,把C(0,3)代入得:a=
x+3;由A(1,0),B(4,0),设抛物线解析式为y=a(x﹣1)(x﹣4)=ax2﹣5ax+4a,把C(0,3)代入得:a=![]() ,则抛物线解析式为y=
,则抛物线解析式为y=![]() x2﹣
x2﹣![]() x+3;(2)存在.如图所示,分三种情况考虑:∵抛物线解析式为y=
x+3;(2)存在.如图所示,分三种情况考虑:∵抛物线解析式为y=![]() x2﹣
x2﹣![]() x+3,∴其对称轴x=﹣
x+3,∴其对称轴x=﹣![]() =﹣
=﹣![]() =
=![]() .当P1C⊥CB时,△P1BC为直角三角形,∵直线BC的斜率为﹣
.当P1C⊥CB时,△P1BC为直角三角形,∵直线BC的斜率为﹣![]() ,两条直线垂直时斜率的积为-1,∴直线P1C斜率为
,两条直线垂直时斜率的积为-1,∴直线P1C斜率为![]() ,∵C(0,3),∴直线P1C解析式为y=
,∵C(0,3),∴直线P1C解析式为y=![]() x+3,与抛物线对称轴方程联立得
x+3,与抛物线对称轴方程联立得 ,解得:
,解得: ,此时P(
,此时P(![]() ,
,![]() );当P2B⊥BC时,△BCP2为直角三角形,同理得到直线P2B的斜率为
);当P2B⊥BC时,△BCP2为直角三角形,同理得到直线P2B的斜率为![]() ,∵B(4,0),∴直线P2B方程为y=
,∵B(4,0),∴直线P2B方程为y=![]() x﹣
x﹣![]() ,与抛物线对称轴方程联立得:
,与抛物线对称轴方程联立得: ,解得:
,解得: ,此时P2(
,此时P2(![]() ,﹣2).∴P1(
,﹣2).∴P1(![]() ,
,![]() )或P2(
)或P2(![]() ,﹣2)时△BCP为直角三角形.当点P为直角顶点,即PC⊥PB时,设P(
,﹣2)时△BCP为直角三角形.当点P为直角顶点,即PC⊥PB时,设P(![]() ,y),∵B(4,0),C(0,3),∴BC=5,∴BC2=PC2+PB2,即25=(
,y),∵B(4,0),C(0,3),∴BC=5,∴BC2=PC2+PB2,即25=(![]() )2+(y﹣3)2+(
)2+(y﹣3)2+(![]() ﹣4)2+y2,解得y=
﹣4)2+y2,解得y=![]() ,∴P3(
,∴P3(![]() ,
,![]() ),P4(
),P4(![]() ,
,![]() )时△BCP为直角三角形..综上所述,在抛物线的对称轴上存在点P,使得以B,C,P三点为顶点的三角形是直角三角形,点P的坐标分别为P1(
)时△BCP为直角三角形..综上所述,在抛物线的对称轴上存在点P,使得以B,C,P三点为顶点的三角形是直角三角形,点P的坐标分别为P1(![]() ,
,![]() ),P2(
),P2(![]() ,﹣2),P3(
,﹣2),P3(![]() ,
,![]() ),P4(
),P4(![]() ,
,![]() ).
).



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在ABCD中,AB=6,AD=8,∠B是锐角,将△ACD沿对角线AC所在直线折叠,点D落在△ABC所在平面内的点E处.如果AE恰好经过BC的中点,那么ABCD的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华民族传统文化,某校举办了“古诗文大赛”,并为获奖同学购买签字笔和笔记本作为奖品.1支签字笔和2个笔记本共8.5元,2支签字笔和3个笔记本共13.5元.
(1)求签字笔和笔记本的单价分别是多少元?
(2)为了激发学生的学习热情,学校决定给每名获奖同学再购买一本文学类且定价为15元的图书,书店出台如下促销方案:购买图书总数超过50本可以享受8折优惠,学校如果多买12本,则可以享受优惠且所花钱数与原来相同,问学校获奖的同学有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 相等的圆心角所对的弧相等
B. 面积相等的两个圆是等圆
C. 三角形的内心到各顶点的距离相等
D. 长度相等的弧是等弧
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家把4,10,16,22,28…叫做等差数列数,根据它的规律,则第100等差数列数为( )
A. 600 B. 2017 C. 602 D. 598
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】统计2010年上海世博会前20天日参观人数,得到如下频数分布表和频数分布直方图(部分未完成): 上海世博会前20天日参观人数的频数分布表:
组别(万人) | 组中值(万人) | 频数 |
7.5~14.5 | 11 | 5 |
14.5~21.5 | 6 | |
21.5~28.5 | 25 | |
28.5~35.5 | 32 | 3 |
上海世博会前20天日参观人数的频数分布直方图: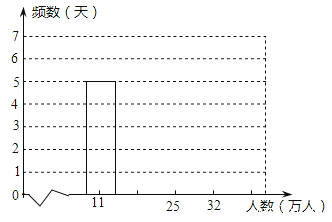
(1)请补全频数分布表和频数分布直方图;
(2)求出日参观人数不低于22万的天数和所占的百分比;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com