
【题目】如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于点Q,当CQ=![]() CE时,EP+BP的值为( )
CE时,EP+BP的值为( )
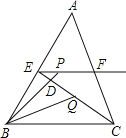
A.6B.9C.12D.18
【答案】C
【解析】
根据平行线和角平分线的性质得到相等的角,然后利用等角对等边,得出BP=PM,从而用其它的线段长表示出EP+BP,再根据线段CQ和CE的关系,得出EQ和CQ的关系,再综合根据平行线得出三角形相似得出EM和BC的关系,从而解决EP+BP的值.
如图,延长BQ交射线EF于M,
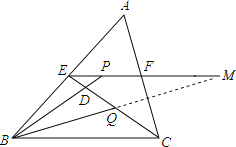
∵E、F分别是AB、AC的中点,
∴EF∥BC,
∴∠M=∠CBM,
∵BQ是∠CBP的平分线,
∴∠PBM=∠CBM,
∴∠M=∠PBM,
∴BP=PM,
∴EP+BP=EP+PM=EM,
∵CQ=![]() CE,
CE,
∴EQ=2CQ,
由EF∥BC得,△MEQ∽△BCQ,
∴![]()
=2,
∴EM=2BC=2×6=12,
即EP+BP=12.
故选:C.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为AC,BD(点A与点B重合),点O是夹子转轴位置,OE⊥AC于点E,OF⊥BD于点F,OE=OF=1cm,AC=BD=6cm, CE=DF, CE:AE=2:3.按图示方式用手指按夹子,夹子两边绕点O转动.
(1)当E,F两点的距离最大值时,以点A,B,C,D为顶点的四边形的周长是_____ cm.
(2)当夹子的开口最大(点C与点D重合)时,A,B两点的距离为_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗击“新冠疫情”期间,某种消毒液A市需要6吨,B市需要8吨,正好M市储备有10吨,N市储备有4吨,预防“新冠疫情”领导小组决定将这14吨消毒液调往A市和B市,消毒液每吨的运费价格如下表。设从M市调运x吨到A市.

(1)求调运14吨消毒液的总运费y关于x的函数关系式;
(2)求出总运费最低的调运方案,最低运费的多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座横跨沙颖河的斜拉桥,拉索两端分别固定在主梁l和索塔h上,索塔h垂直于主梁l,垂足为D.拉索AE,BF,CG的仰角分别是α,45°,β,且α+β=90°(α<β),AB=15m,BC=5m,CD=4m,EF=3FG,求拉索AE的长.(精确到1m,参考数据:![]() ≈2.24,
≈2.24,![]() ≈1.41)
≈1.41)
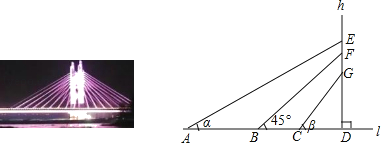
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组为了解本校七年级女生的身高情况,统计了甲、乙两个班女生的身高,并绘制了以下不完整的统计图.(身高单位:![]() )
)

请根据图中信息,解答下列问题:
(1)两个班共有女生 人;
(2)将频数分布直方图补充完整;
(3)求扇形统计图中![]() 部分所对应的扇形圆心角度数;
部分所对应的扇形圆心角度数;
(4)该校七年级共有女生![]() 人,请估计身高在
人,请估计身高在![]() 范围的女生人数.
范围的女生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是边长为2的等边三角形,点
是边长为2的等边三角形,点![]() 与点
与点![]() 分别位于直线
分别位于直线![]() 的两侧,且
的两侧,且![]() ,连接
,连接![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)当![]() 时,求线段
时,求线段![]() 的长;
的长;
(2)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,
,
①当![]() 时,设
时,设![]() (其中
(其中![]() 表示
表示![]() 的面积,
的面积,![]() 表示
表示![]() 的面积),求
的面积),求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
②当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长.
的长.
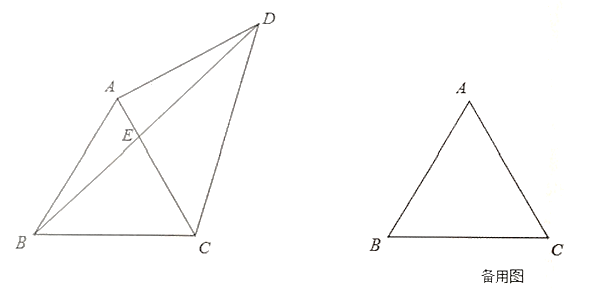
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与x轴交于点A,与y轴交于点B,直线
与x轴交于点A,与y轴交于点B,直线![]() 与x轴交于点C.
与x轴交于点C.

(1)求点B的坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 围成的区域(不含边界)为G.
围成的区域(不含边界)为G.
①当![]() 时,结合函数图象,求区域G内整点的个数;
时,结合函数图象,求区域G内整点的个数;
②若区域G内恰有2个整点,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
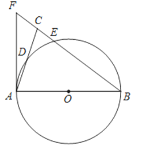
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE,AF的长.
,CE:EB=1:4,求CE,AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
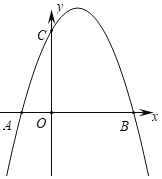
【题目】如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0),OB=OC=3OA.若抛物线L2与抛物线L1关于直线x=2对称.
(1)求抛物线L1与抛物线L2的解析式;
(2)在抛物线L1上是否存在一点P,在抛物线L2上是否存在一点Q,使得以BC为边,且以B、C、P、Q为顶点的四边形为平行四边形?若存在,求出P、Q两点的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com