
【题目】已知⊙O1和⊙O2外切于M,AB是⊙O1和⊙O2的外公切线,A,B为切点,若MA=4cm,MB=3cm,则M到AB的距离是( )
A. ![]() cm B.
cm B. ![]() cm C.
cm C. ![]() cm D.
cm D. ![]() cm
cm
【答案】B
【解析】
先画图,由AB是⊙O1和⊙O2的外公切线,则∠O1AB=∠O2BA=90°,再由O1A=O1M,O2B=O2M,得∠O1AM=∠O1MA,∠O2BM=∠O2MB,则∠BAM+∠AMO1=90°,∠ABM+∠BMO2=90°,则∠BMO2+∠AMO1=90°,从而∠AMB=90°,再由勾股定理求出AB的长,然后由面积法可求出AB边上的高.
如图,
∵AB是⊙O1和⊙O2的外公切线,
∴∠O1AB=∠O2BA=90°,
∵O1A=O1M,O2B=O2M,
∴∠O1AM=∠O1MA,∠O2BM=∠O2MB,
∴∠BAM+∠AMO1=90°,∠ABM+∠BMO2=90°,
∴∠BAM+∠AMO1+∠ABM+∠BMO2=180°,
∴∠BMO2+∠AMO1=90°,
∴∠AMB=90°,
∴AM⊥BM,
∴△ABM是直角三角形,
∵MA=4cm,MB=3cm,
∴由勾股定理得,AB=![]() =5cm,
=5cm,
由三角形的面积公式,M到AB的距离是![]() cm,
cm,
故选:B.


科目:初中数学 来源: 题型:
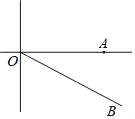
【题目】如图,A城气象台测得台风中心在A城正西方向240km的O处,以每小时30km的速度向南偏东60°的OB方向移动,距台风中心150km的范围内是受台风影响的区域.
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到台风的影响,求出受台风影响的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:对于一个关于![]() 的一元二次方程
的一元二次方程![]() (其中a≠0,a、b、c为常数)的两根分别为
(其中a≠0,a、b、c为常数)的两根分别为![]() ,
,![]() ,我们有如下发现①若
,我们有如下发现①若![]() ,
,![]() 为整数,则这个一元二次方程的判别式
为整数,则这个一元二次方程的判别式![]() 一定为完全平方数;②
一定为完全平方数;② ![]() ,
,![]() 满足韦达定理:即
满足韦达定理:即![]() ,
,![]() ;
;
③韦达定理也有逆定理,即如果两数![]() 和
和![]() 满足如下关系:
满足如下关系:![]() ,
,![]() ,那么这两个数
,那么这两个数![]() 和
和![]() 是方程
是方程![]() (
(![]() )的两个根.
)的两个根.
请应用上述材料解决以下问题:
(1)若实数![]() ,
,![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,
的两个根,
①当![]() 时,则
时,则![]() ,
,![]() ;
;
②若![]() 均为整数且
均为整数且![]() ,求
,求![]() 的值;
的值;
(2)已知实数![]() 满足
满足![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
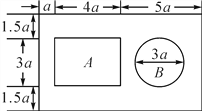
【题目】某居民小区响应党的号召,开展全民健身活动.该小区准备修建一座健身馆,其设计方案如图所示,A区为成年人活动场所,B区为未成年人活动场所,其余地方均种花草.(π取3.14)
(1)活动场所和花草的面积各是多少?
(2)整座健身馆的面积是成年人活动场所面积的多少倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮计划暑期结伴参加志愿者活动.小明想参加敬老服务活动,小亮想参加文明礼仪宣传活动.他们想通过做游戏来决定参加哪个活动,于是小明设计了一个游戏,游戏规则是:在三张完全相同的卡片上分别标记4、5、6三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则按照小明的想法参加敬老服务活动,若抽出的两张卡片标记的数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
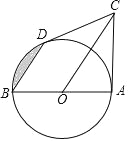
【题目】如图,AB是⊙O的直径,CD切⊙O于点D,且BD∥OC,连接AC.
(1)求证:AC是⊙O的切线;
(2)若AB=OC=4,求图中阴影部分的面积(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
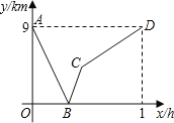
【题目】小明骑电动车从甲地去乙地,而小刚骑自行车从乙地去甲地,两人同时出发走相同的路线;设小刚行驶的时间为x(h),两人之间的距离为y(km),图中的折线表示y与x之间的函数关系,点B的坐标为(![]() ,0).根据图象进行探究:
,0).根据图象进行探究:
(1)两地之间的距离为______km;
(2)请解释图中点B的实际意义;
(3)求两人的速度分别是每小时多少km?
(4)直接写出点C的坐标______.
查看答案和解析>>
科目:初中数学 来源: 题型:
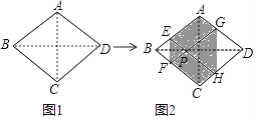
【题目】如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
①当x=1时,点P是菱形ABCD的中心;②当x= ![]() 时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是
时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是 ![]() ;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确结论是________.(填序号)
;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确结论是________.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com