
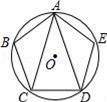
如图,正五边形ABCDE内接于⊙O,则∠CAD= 度.

科目:初中数学 来源: 题型:
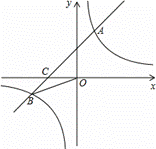
已知:如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比
例函数y=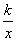 的图象分别交于第一、三象限内的A、B两点,与x轴交于C点,
的图象分别交于第一、三象限内的A、B两点,与x轴交于C点,
点A的坐标(2,m),点B的坐标为(n,-2),tan∠BOC=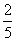
(1)求该反比例函数与一次函数的表达式;
(2)在x轴上有一点E(不与O重合),使得△BCE与△BCO
的面积相等,求出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB、CD交于点O,∠AOE=90°,若∠AOC:∠COE=5:4,则∠AOD等于( )
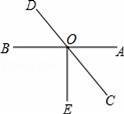

A.150° B.140° C.120° D.130°
查看答案和解析>>
科目:初中数学 来源: 题型:
操作:某数学兴趣小组在研究用一副三角板拼角时,小明、小亮分别拼出图1、图2所示的两种图形,如图1,小明把30°和90°的角按如图1方式拼在一起;小亮把30°和90°的角按如图2方式拼在一起,并在各自所拼的图形中分别作出∠AOB、∠COD的平分线OE、OF.小明很容易地计算出图1中∠EOF=60°.
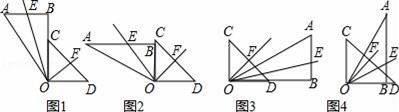

计算:请你计算出图2中∠EOF= 度.
归纳:通过上面的计算猜一猜,当有公共顶点的两个角∠α、∠β有一条边重合,且这两个角在公共边的异侧时,则这两个角的平分线所夹的角= .(用含α、β的代数式表示)
拓展:小明把图1中的三角板AOB绕点O顺时针旋转90°后得到图3,小亮把图2中的三角板AOB绕点O顺时针旋转90°后得到图4(两图中的点O、B、D在同一条直线上).在图3中,易得到∠EOF=∠DOF﹣∠BOE=
 ∠COD﹣
∠COD﹣
 ∠AOB=45°﹣15°=30°;仿照图3的作法,请你通过计算,求出图4中∠EOF的度数(写出解答过程).
∠AOB=45°﹣15°=30°;仿照图3的作法,请你通过计算,求出图4中∠EOF的度数(写出解答过程).
反思:通过上面的拓展猜一猜,当有公共顶点的两个角∠α、∠β(∠α>∠β)有一条边重合,且这两个角在公共边的同侧时,则这两个角的平分线所夹的角= .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,二次函数y=ax2+bx+c的图象与x轴相交于(﹣2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是( )
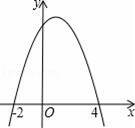

A.x<﹣2 B.﹣2<x<4 C.x>0 D.x>4
查看答案和解析>>
科目:初中数学 来源: 题型:
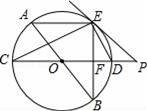
如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com