
ВйзїЃКФГЪ§бЇаЫШЄаЁзщдкбаОПгУвЛИБШ§НЧАхЦДНЧЪБЃЌаЁУїЁЂаЁССЗжБ№ЦДГіЭМ1ЁЂЭМ2ЫљЪОЕФСНжжЭМаЮЃЌШчЭМ1ЃЌаЁУїАб30ЁуКЭ90ЁуЕФНЧАДШчЭМ1ЗНЪНЦДдквЛЦ№ЃЛаЁССАб30ЁуКЭ90ЁуЕФНЧАДШчЭМ2ЗНЪНЦДдквЛЦ№ЃЌВЂдкИїздЫљЦДЕФЭМаЮжаЗжБ№зїГіЁЯAOBЁЂЁЯCODЕФЦНЗжЯпOEЁЂOFЃЎаЁУїКмШнвзЕиМЦЫуГіЭМ1жаЁЯEOF=60ЁуЃЎ
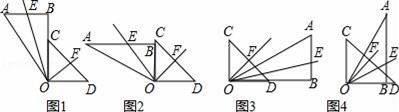

МЦЫуЃКЧыФуМЦЫуГіЭМ2жаЁЯEOF=ЁЁЁЁЁЁЁЁЁЁЁЁЖШЃЎ
ЙщФЩЃКЭЈЙ§ЩЯУцЕФМЦЫуВТвЛВТЃЌЕБгаЙЋЙВЖЅЕуЕФСНИіНЧЁЯІСЁЂЁЯІТгавЛЬѕБпжиКЯЃЌЧветСНИіНЧдкЙЋЙВБпЕФвьВрЪБЃЌдђетСНИіНЧЕФЦНЗжЯпЫљМаЕФНЧ=ЁЁЁЁЁЁЁЁЁЁЁЁЃЎЃЈгУКЌІСЁЂІТЕФДњЪ§ЪНБэЪОЃЉ
ЭиеЙЃКаЁУїАбЭМ1жаЕФШ§НЧАхAOBШЦЕуOЫГЪБеыа§зЊ90ЁуКѓЕУЕНЭМ3ЃЌаЁССАбЭМ2жаЕФШ§НЧАхAOBШЦЕуOЫГЪБеыа§зЊ90ЁуКѓЕУЕНЭМ4ЃЈСНЭМжаЕФЕуOЁЂBЁЂDдкЭЌвЛЬѕжБЯпЩЯЃЉЃЎдкЭМ3жаЃЌвзЕУЕНЁЯEOF=ЁЯDOFЉЁЯBOE=
 ЁЯCODЉ
ЁЯCODЉ
 ЁЯAOB=45ЁуЉ15Ёу=30ЁуЃЛЗТееЭМ3ЕФзїЗЈЃЌЧыФуЭЈЙ§МЦЫуЃЌЧѓГіЭМ4жаЁЯEOFЕФЖШЪ§ЃЈаДГіНтД№Й§ГЬЃЉЃЎ
ЁЯAOB=45ЁуЉ15Ёу=30ЁуЃЛЗТееЭМ3ЕФзїЗЈЃЌЧыФуЭЈЙ§МЦЫуЃЌЧѓГіЭМ4жаЁЯEOFЕФЖШЪ§ЃЈаДГіНтД№Й§ГЬЃЉЃЎ
ЗДЫМЃКЭЈЙ§ЩЯУцЕФЭиеЙВТвЛВТЃЌЕБгаЙЋЙВЖЅЕуЕФСНИіНЧЁЯІСЁЂЁЯІТЃЈЁЯІСЃОЁЯІТЃЉгавЛЬѕБпжиКЯЃЌЧветСНИіНЧдкЙЋЙВБпЕФЭЌВрЪБЃЌдђетСНИіНЧЕФЦНЗжЯпЫљМаЕФНЧ=ЁЁЁЁЁЁЁЁЁЁЁЁЃЎ
ЁЁ
ЁОПМЕуЁПНЧЕФМЦЫуЃЛНЧЦНЗжЯпЕФЖЈвхЃЎ
ЁОЗжЮіЁПМЦЫуКЭЙщФЩЃКИљОнНЧЦНЗжЯпЕФЖЈвхКЭНЧЕФЮЛжУЙиЯЕПЩвдЧѓЕУЃКЁЯAOE=ЁЯEOB=
 ЁЯAOBЃЌЁЯCOF=ЁЯFOD=
ЁЯAOBЃЌЁЯCOF=ЁЯFOD=
 ЁЯCODЃЌдйИљОнЁЯEOF=ЁЯEOB+ЁЯBOFПЩвдЧѓЕУЁЯEOFЕФЖШЪ§ЃЛЭиеЙКЭЗДЫМЃКИљОнНЧЦНЗжЯпЕФЖЈвхКЭНЧЕФЮЛжУЙиЯЕПЩвдЧѓЕУЃКЁЯAOE=ЁЯEOB=
ЁЯCODЃЌдйИљОнЁЯEOF=ЁЯEOB+ЁЯBOFПЩвдЧѓЕУЁЯEOFЕФЖШЪ§ЃЛЭиеЙКЭЗДЫМЃКИљОнНЧЦНЗжЯпЕФЖЈвхКЭНЧЕФЮЛжУЙиЯЕПЩвдЧѓЕУЃКЁЯAOE=ЁЯEOB=
 ЁЯAOBЃЌЁЯCOF=ЁЯFOD=
ЁЯAOBЃЌЁЯCOF=ЁЯFOD=
 ЁЯCODЃЌдйИљОнЁЯEOF=ЁЯBOFЉЁЯBOEПЩвдЧѓЕУЁЯEOFЕФЖШЪ§ЃЎ
ЁЯCODЃЌдйИљОнЁЯEOF=ЁЯBOFЉЁЯBOEПЩвдЧѓЕУЁЯEOFЕФЖШЪ§ЃЎ
ЁОНтД№ЁПНтЃКМЦЫуЃКЁпЁЯAOC=60ЁуЃЌЁЯCOD=90ЁуЃЌ
ЁпOEЁЂOFЗжБ№ЦНЗжЁЯAOBЁЂЁЯCODЃЌ
ЁрЁЯAOE=ЁЯEOB=
 ЁЯAOBЃЌЁЯCOF=ЁЯFOD=
ЁЯAOBЃЌЁЯCOF=ЁЯFOD=
 ЁЯCODЃЌ
ЁЯCODЃЌ
ЁрЁЯEOF=ЁЯBOE+ЁЯCOF=75ЁуЃЌ
ЙЪД№АИЮЊЃК75ЁуЃЛ
ЙщФЩЃК
 ЃЛ
ЃЛ
ЙЪД№АИЮЊЃК
 ЃЛ
ЃЛ
ЭиеЙЃКЁпOEЁЂOFЗжБ№ЦНЗжЁЯAOBЁЂЁЯCODЃЌ
Ёр
 =30ЁуЃЌ
=30ЁуЃЌ
 ЃЌ
ЃЌ
ЁрЁЯEOF=ЁЯDOFЉЁЯDOE=15ЁуЃЛ
ЗДЫМЃК
 ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК
 ЃЎ
ЃЎ
ЁОЕуЦРЁПДЫЬтжївЊПМВщСЫНЧЕФМЦЫуЃЌЙиМќЪЧзЂвтДЫЬтЗжСНжжЧщПіЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
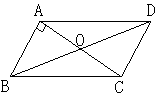
ШчЭМЁѕABCDЕФЖдНЧЯпACгыBDЯрНЛгкЕуOЃЌABЁЭACЃЌAB=4ЃЌAC=6ЃЌ
дђBDЕФГЄЮЊЃЈ ЃЉ
AЁЂ8 BЁЂ9 CЁЂ10 DЁЂ11
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ФГЭЌбЇдкЖдЗНГЬ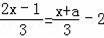
 ШЅЗжФИЪБЃЌЗНГЬгвБпЕФЉ2УЛгаГЫ3ЃЌетЪБЗНГЬЕФНтЮЊx=2ЃЌЪдЧѓaЕФжЕЃЌВЂЧѓГідЗНГЬе§ШЗЕФНтЃЎ
ШЅЗжФИЪБЃЌЗНГЬгвБпЕФЉ2УЛгаГЫ3ЃЌетЪБЗНГЬЕФНтЮЊx=2ЃЌЪдЧѓaЕФжЕЃЌВЂЧѓГідЗНГЬе§ШЗЕФНтЃЎ
ЁЁ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ФГЮФЛЏЩЬГЁЭЌЪБТєГіСНЬЈЕчзгЧйЃЌУПЬЈОљТє960дЊЃЎвдГЩБОМЦЫуЃЌЕквЛЬЈгЏРћ20%ЃЌСэвЛЬЈПїБО20%ЃЎдђБОДЮГіЪлжаЃЌЩЬГЁЃЈЁЁЁЁЃЉ
AЃЎВЛзЌВЛХт BЃЎзЌ160дЊ CЃЎзЌ80дЊ DЃЎХт80дЊ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ШчЭМЃЌAЃЌBЃЌCШ§ЕудкЁбOЩЯЃЌЧвЁЯBOC=100ЁуЃЌдђЁЯAЕФЖШЪ§ЮЊЃЈЁЁЁЁЃЉ
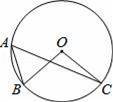

AЃЎ40Ёу BЃЎ50Ёу CЃЎ80Ёу DЃЎ100Ёу
ЁЁ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
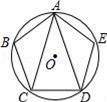
ШчЭМЃЌе§ЮхБпаЮABCDEФкНггкЁбOЃЌдђЁЯCAD=ЁЁЁЁЁЁЁЁЁЁЁЁЖШЃЎ

ЁЁ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
вЛдЊЖўДЮЗНГЬx2Љ2ЃЈ3xЉ2ЃЉ+ЃЈx+1ЃЉ=0ЕФвЛАуаЮЪНЪЧЃЈЁЁЁЁЃЉ
AЃЎx2Љ5x+5=0 BЃЎx2+5xЉ5=0 CЃЎx2+5x+5=0 DЃЎx2+5=0
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com