
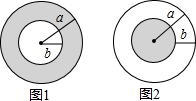
 如图1,在一个半径为a的大圆内,挖去一个半径为b(0<b<a)的小圆,剩下部分(阴影部分)的面积为S1;如图2,在一个半径为a的大圆上剪去一个圆环(内径为b),剩下部分(阴影部分)的面积为S2,则S1与S2的大小关系是( )
如图1,在一个半径为a的大圆内,挖去一个半径为b(0<b<a)的小圆,剩下部分(阴影部分)的面积为S1;如图2,在一个半径为a的大圆上剪去一个圆环(内径为b),剩下部分(阴影部分)的面积为S2,则S1与S2的大小关系是( )| A. | S1>S2 | B. | S1≥S2 | C. | S1<S2 | D. | S1≤S2 |
分析 图1中圆环面积=大圆面积-小圆面积,图2中半径为a-b的小圆面积根据圆的面积公式列式可得,然后利用作差比较法比较大小即可.
解答 解:在一个半径为a的大圆内,挖去一个半径为b(0<b<a)的小圆,剩下部分(阴影部分)的面积为S1=$\frac{1}{2}π{a}^{2}-\frac{1}{2}π{b}^{2}$,
在一个半径为a的大圆上剪去一个圆环(内径为b),剩下部分(阴影部分)的面积为S2=$\frac{1}{2}π(a-b)^{2}$,
因为S1-S2=$\frac{1}{2}π{a}^{2}-\frac{1}{2}π{b}^{2}$-$\frac{1}{2}π(a-b)^{2}$
=$\frac{1}{2}$π[a2-b2-(a-b)2]
=$\frac{1}{2}$π(a2-b2-a2+2ab-b2)
=$\frac{1}{2}π(2ab-2{b}^{2})$
=πb(a-b),
∵0<b<a,
∴πb(a-b)>0,
∴S1>S2,
故选:A.
点评 本题主要考查列代数式及作差法比较大小,根据题意列出代数式是解题的前提和根本,通过作差法比较两代数式的大小是关键.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
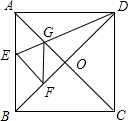 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:①∠AGD=112.5°;②AD=2AE;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的序号是( )
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:①∠AGD=112.5°;②AD=2AE;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的序号是( )| A. | ①②③ | B. | ①③④ | C. | ①④⑤ | D. | ①②③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{8}{x}+\frac{5}{x-3}=1$ | B. | $(\frac{1}{x}+\frac{1}{x+3})×5+\frac{3}{x}=1$ | C. | $\frac{3}{x-3}+5(\frac{1}{x-3}+\frac{1}{x})=1$ | D. | $\frac{5}{x+(x+3)}+\frac{3}{x}=1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲品牌 | 乙品牌 | |
| 进价(元/件) | 1100 | 1400 |
| 售价(元/件) | - | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
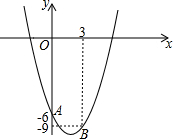 如图,已知抛物线y=ax2-4x+c经过点A(0,-6)和B(3,-9).
如图,已知抛物线y=ax2-4x+c经过点A(0,-6)和B(3,-9).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com