
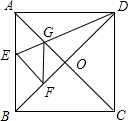
 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:①∠AGD=112.5°;②AD=2AE;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的序号是( )
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:①∠AGD=112.5°;②AD=2AE;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的序号是( )| A. | ①②③ | B. | ①③④ | C. | ①④⑤ | D. | ①②③④⑤ |
分析 ①根据正方形性质和折叠性质得出∠GAD和∠ADG,即可求解;
②根据直角三角形的直角边小于斜边,即可得出结论;
③根据角平分线的性质得出三角形的高相等,再分析底边长即可;
④证明四条边相等即可;
⑤由折叠的性质设BF=EF=AE=1,进一步表示AB,BD,DF的长度,结合相似三角形进行求解即可.
解答 解:因为在正方形纸片ABCD中,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,
所以∠GAD=45°,∠ADG=$\frac{1}{2}∠ADO=22.5°$,
可求,∠AGD=112.5°,所以①正确.
因为tan∠AED=$\frac{AD}{AE}$,
因为AE=EF<BE,
所以AE<$\frac{1}{2}$AB,
因为AD=AB,因此②错.
因为AG=FG>OG,△AGD与△OGD同高,
所以S△AGD>S△OGD,所以③错.
根据题意可得:AE=EF,AG=FG,又因为EF∥AC,
所以∠FEG=∠AGE,又因为∠AEG=∠FEG,
所以∠AEG=∠AGE,所以AE=AG=EF=FG,
所以四边形AEFG是菱形,因此④正确.
由折叠的性质设BF=EF=AE=1,则AB=1+$\sqrt{2}$,BD=2+$\sqrt{2}$,DF=1+$\sqrt{2}$,
由此可求,
$\frac{OG}{EF}$=$\frac{\sqrt{2}}{2}$,
因为EF∥AC,
所以△DOG∽△DFE,
所以$\frac{OG}{EF}=\frac{DO}{DF}=\frac{\sqrt{2}}{2}$,
∴$\sqrt{2}$EF=2OG,
在直角三角形BEF中,∠EBF=45°,
所以△BEF是等腰直角三角形,同理可证△OFG是等腰直角三角形,
在等腰直角三角形BEF和等腰直角三角形OFG中,BE2=2EF2=2GF2=2×2OG2,
所以BE=2OG.因此⑤正确.
故答案为:C.
点评 此题主要考查四边形综合问题,熟悉正方形性质和菱形的判定,会用勾股定理进行线段求值,会根据平行论证相似是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 开口向上,顶点($\frac{1}{2}$,-$\frac{5}{4}$) | B. | 开口向下,顶点($\frac{1}{2}$,-$\frac{5}{4}$) | ||
| C. | 开口向上,顶点(-$\frac{1}{2}$,$\frac{5}{4}$) | D. | 开口向下,顶点(-$\frac{1}{2}$,$\frac{5}{4}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
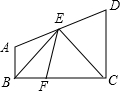 如图,四边形ABCD中,AB∥DC,E是AD上一点,且BE平分∠ABC,CE平分∠BCD,在BC上取一点F,使BF=AB
如图,四边形ABCD中,AB∥DC,E是AD上一点,且BE平分∠ABC,CE平分∠BCD,在BC上取一点F,使BF=AB查看答案和解析>>
科目:初中数学 来源: 题型:选择题
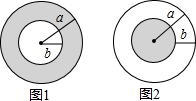 如图1,在一个半径为a的大圆内,挖去一个半径为b(0<b<a)的小圆,剩下部分(阴影部分)的面积为S1;如图2,在一个半径为a的大圆上剪去一个圆环(内径为b),剩下部分(阴影部分)的面积为S2,则S1与S2的大小关系是( )
如图1,在一个半径为a的大圆内,挖去一个半径为b(0<b<a)的小圆,剩下部分(阴影部分)的面积为S1;如图2,在一个半径为a的大圆上剪去一个圆环(内径为b),剩下部分(阴影部分)的面积为S2,则S1与S2的大小关系是( )| A. | S1>S2 | B. | S1≥S2 | C. | S1<S2 | D. | S1≤S2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线相等的四边形是矩形 | |
| B. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| C. | 对角线互相垂直平分的四边形是菱形 | |
| D. | 一组邻边相等,并且有一个内角为直角的四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com