
【题目】解下列不等式,并把(1)解集表示在数轴上.
(1)4x+5≥6x-3.
(2)![]()
(3)解下列不等式组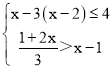
(4)解不等式组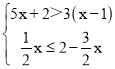 ,并写出它的所有整数解.
,并写出它的所有整数解.
【答案】(1)x≤4,数轴见解析;(2)x≤-1;(3)1≤x<4;(4)![]() <x≤1,-2,-1,0,1
<x≤1,-2,-1,0,1
【解析】
(1)移项、合并同类项,把x的系数化为1,再在数轴上表示出来即可;
(2)先去分母,再去括号,移项、合并同类项,把x的系数化为1;
(3)分别求出各不等式的解集,再求出其公共解集
(4)分别求出各不等式的解集,再求出其公共解集.
解:(1)移项得,4x-6x≥-3-5,
合并同类项得,-2x≥-8,
把x的系数化为1得,x≤4.
在数轴上表示为:
![]() ;
;
(2)![]()
去分母得,2(2x-1)-3(5x+1)≥6
去括号得,4x-2-15x-3≥6,
移项得,4x-15x≥6+2+3,
合并同类项得,-11x≥11,
把x的系数化为1得,x≤-1.
(3)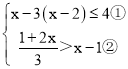
由①得,x≥1,
由②得,x<4,
故不等式组的解集为:1≤x<4.
(4)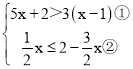
由①得,x>-![]() ,
,
由②得,x≤1,
所以不等式组的解集为:-![]() <x≤1,
<x≤1,
故它的所有整数解为:-2,-1,0、1.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
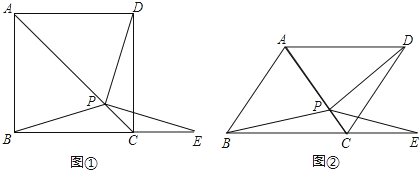
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下列材料,然后完成解答:
(材料)
如图,已知平面直角坐标系中两点A(x1,y1)、B(x2,y2),如何求A、B两点间的的距离|AB|的值?
过点A向y轴作垂线AN1、过点B向x轴作垂线BM2,垂足分别为N1(0,y1)和M2(x2,0),直线AN1和BM2相交于点Q.
在Rt△AQB中,|AB|2= |AQ|2+ |BQ|2
为了计算AQ和BQ,过点A向x轴作垂线,垂足为M1(x1,0);过点B向y轴作垂线,垂足为N2(0,y2),于是有|AQ|=|M1M2|=|x3-x1|,|BQ|=|N1N2|=|y2-y1|.
所以,|AB|2=![]() .
.
由此得到A(x1,y1)、B(x2,y2)两点间的距离公式:![]() .
.
根据定义:两点之间线段的长度,叫做这两点之间的距离.
因此,线段AB的长度计算公式为![]() .
.
(问题)
(1)平面直角坐标系中有两点A(0,1)、B(2,3),求线段AB的长;
(2)![]() 表示线段MN的长,其中点M的坐标为(a,b),点N的坐标为______;
表示线段MN的长,其中点M的坐标为(a,b),点N的坐标为______;
(3)如图,在x轴上有一点P(x,0),试求PA+PB的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形![]() 的边长
的边长![]() .某一时刻,动点
.某一时刻,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动;同时,动点
点匀速运动;同时,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动,问:
点匀速运动,问:
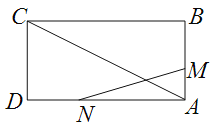
(1)经过多少时间,![]() 的面积等于矩形
的面积等于矩形![]() 面积的
面积的![]() ?
?
(2)是否存在时刻t,使以A,M,N为顶点的三角形与![]() 相似?若存在,求t的值;若不存在,请说明理由.
相似?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
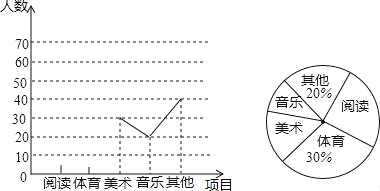
【题目】某学校为了解学生的课余活动情况,抽样调查了部分学生,将所得数据处理后,制成折线统计图(部分)和扇形统计图(部分)如图:
(1)在这次研究中,一共调查了 学生,并请补全折线统计图;
(2)该校共有2200名学生,估计该校爱好阅读和爱好体育的学生一共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
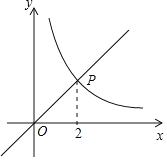
【题目】如图,函数y=x的图象与函数y=![]() (x>0)的图象相交于点P(2,m).
(x>0)的图象相交于点P(2,m).
(1)求m,k的值;
(2)直线y=4与函数y=x的图象相交于点A,与函数y=![]() (x>0)的图象相交于点B,求线段AB长.
(x>0)的图象相交于点B,求线段AB长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习完第十二章后,张老师让同学们独立完成课本56页第9题:“如图1,![]() ,
,![]() ,
,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.”
的长.”

(1)请你也独立完成这道题:
(2)待同学们完成这道题后,张老师又出示了一道题:
在课本原题其它条件不变的前提下,将![]() 所在直线旋转到
所在直线旋转到![]() 的外部(如图2),请你猜想
的外部(如图2),请你猜想![]() ,
,![]() ,
,![]() 三者之间的数量关系,直接写出结论:_______.(不需证明)
三者之间的数量关系,直接写出结论:_______.(不需证明)
(3)如图3,将(1)中的条件改为:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=
三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=![]() ,其中
,其中![]() 为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由:
为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com