
【题目】认真阅读下列材料,然后完成解答:
(材料)
如图,已知平面直角坐标系中两点A(x1,y1)、B(x2,y2),如何求A、B两点间的的距离|AB|的值?
过点A向y轴作垂线AN1、过点B向x轴作垂线BM2,垂足分别为N1(0,y1)和M2(x2,0),直线AN1和BM2相交于点Q.
在Rt△AQB中,|AB|2= |AQ|2+ |BQ|2
为了计算AQ和BQ,过点A向x轴作垂线,垂足为M1(x1,0);过点B向y轴作垂线,垂足为N2(0,y2),于是有|AQ|=|M1M2|=|x3-x1|,|BQ|=|N1N2|=|y2-y1|.
所以,|AB|2=![]() .
.
由此得到A(x1,y1)、B(x2,y2)两点间的距离公式:![]() .
.
根据定义:两点之间线段的长度,叫做这两点之间的距离.
因此,线段AB的长度计算公式为![]() .
.
(问题)
(1)平面直角坐标系中有两点A(0,1)、B(2,3),求线段AB的长;
(2)![]() 表示线段MN的长,其中点M的坐标为(a,b),点N的坐标为______;
表示线段MN的长,其中点M的坐标为(a,b),点N的坐标为______;
(3)如图,在x轴上有一点P(x,0),试求PA+PB的最小值.

【答案】(1)AB=![]() ;(2)(-2,0);(3)
;(2)(-2,0);(3)![]() .
.
【解析】
(1)利用两点间的距离公式![]() 进行计算即可;
进行计算即可;
(2)由点M坐标为(a,b),可将MN变化为![]() ,可得点N坐标为(-2,0);
,可得点N坐标为(-2,0);
(3)作点A关于x轴的对称点A′,连接BA′,直线BA′于x轴的交点即为所求的点P,AP=A′P,A′B=A′P+BP=PA+PB,根据两点之间,线段最短,可得A′B等于PA+PB的最小值;
解:
(1)将点A(0,1)、B(2,3)代入![]() 得,
得,
![]() =
=![]() =
=![]() =
=![]() ;
;
∴AB的长为![]() ;
;
(2)由题可知,![]() ,点M坐标为(a,b),
,点M坐标为(a,b),
∴![]() ,
,
∴点N坐标为(-2,0);
(3)如图:作点A关于x轴的对称点A′(0,-1),连接A′B,交x轴于点P,可得,AP=A′P,A′B=A′P+BP=PA+PB,
根据两点之间,线段最短,可得A′B等于PA+PB的最小值.
![]() =
=![]() =
=![]() =
=![]() ;
;


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
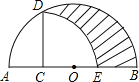
【题目】如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=4,则图中阴影部分的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
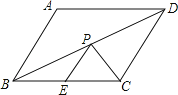
【题目】如图,菱形ABCD的边长是4cm,且∠ABC=60°,E是BC中点,P点在BD上,则PE+PC的最小值为( )cm.
A.2B.2![]() C.3D.4
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() (0,
(0, ![]() )
)![]() .
.
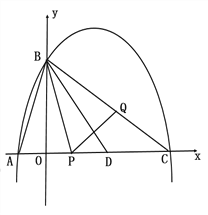
(1)求抛物线的解析式.
(2)抛物线与![]() 轴交于另一个交点为C,点D在线段AC上,已知AD=AB,若动点P从A出发沿线段AC以每秒1个单位长度的速度匀速运动,同时另一个动点Q以某一速度从B出发沿线段BC匀速运动,问是否存在某一时刻,使线段PQ被直线BD垂直平分,若存在,求出点Q的运动速度;若不存在,请说明理由.
轴交于另一个交点为C,点D在线段AC上,已知AD=AB,若动点P从A出发沿线段AC以每秒1个单位长度的速度匀速运动,同时另一个动点Q以某一速度从B出发沿线段BC匀速运动,问是否存在某一时刻,使线段PQ被直线BD垂直平分,若存在,求出点Q的运动速度;若不存在,请说明理由.
(3)在(2)的前提下,过点B的直线![]() 与
与![]() 轴的负半轴交于点M,是否存在点M,使以A、B、M为顶点的三角形与
轴的负半轴交于点M,是否存在点M,使以A、B、M为顶点的三角形与![]() 相似,如果存在,请直接写出M的坐标;若不存在,请说明理由.
相似,如果存在,请直接写出M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(1,4),C(3,1).
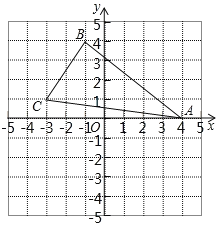
(1)在图中作△A′B′C′,使△A′B′C′和△ABC关于x轴对称;
(2)写出点B′的坐标_________;
(3) △A′B′C′的面积为________平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
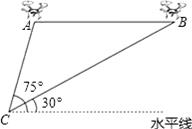
【题目】某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com