练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图在平面直角坐标系中，△ABC各顶点的坐标分别为：A(4，0)，B(1，4)，C(3，1)．

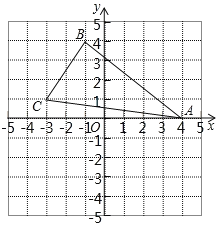
    (1)在图中作△A′B′C′，使△A′B′C′和△ABC关于x轴对称；

    (2)写出点B′的坐标_________；

    (3) △A′B′C′的面积为________平方单位．

    【答案】（1）见解析；（2）（－1，－4）；（3）11.5．

    【解析】

    （1）直接利用关于x轴对称点的性质，进而得出答案；

    （2）直接利用（1）中所画图形得出B′的坐标即可；

    （3）利用△ABC所在矩形面积减去周围三角形面积进而得出答案．

    解：

    （1）如图：△A′B′C′即为所求，

    （2）由（1）可得，点B′的坐标为(1，4)；

    （3）△ABC的面积为：7×4×2×3×4×5×1×7=11.5；

    ∴△ABC的面积为11.5；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，点O为对角线AC的中点，过O点的射线OM，ON分别交AB，BC于点E，F，且∠EOF=90°，BO，EF交于点P，则下面结论：

    ①图形中全等的三角形只有三对；②△EOF是等腰直角三角形；③正方形ABCD的面积等于四边形OEBF面积的4倍；④BE＋BF=OA．

    其中正确结论的个数是(　　)

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司销售部有营销人员15人，销售部为了制定某种商品的月销售定额，统计了这15人某月的销售如下:

    每人销售件数

    1800

    510

    250

    210

    150

    120

    人数

    1

    1

    3

    5

    3

    2

    （1）求这15位营销人员该月销售量的平均数、中位数和众数.

    （2）假设销售部负责人把每位营销员的月销售额定为320件，你认为是否合理?为什么?如不合理，请你制定一个合理的销售定额，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠B=90°，AB=12，BC=24，动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动，动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动，如果点P、Q分别从点A、B同时出发，那么△PBQ的面积S随出发时间t（s）如何变化？写出函数关系式及t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某中学准备在校园里利用院墙的一段再围三面篱笆，形成一个矩形花园ABC（院墙 MN 长 25 米）．现有 50米长的篱笆，请你设计一种围法（篱笆必须用完），使矩形花园的面积为300米 2．

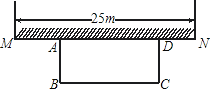
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】认真阅读下列材料，然后完成解答：

    （材料）

    如图，已知平面直角坐标系中两点A（x1，y1）、B（x2，y2），如何求A、B两点间的的距离|AB|的值？

    过点A向y轴作垂线AN1、过点B向x轴作垂线BM2，垂足分别为N1（0，y1）和M2（x2，0），直线AN1和BM2相交于点Q．

    在Rt△AQB中，|AB|2= |AQ|2+ |BQ|2

    为了计算AQ和BQ，过点A向x轴作垂线，垂足为M1（x1，0）；过点B向y轴作垂线，垂足为N2（0，y2），于是有|AQ|=|M1M2|=|x3-x1|，|BQ|=|N1N2|=|y2-y1|．

    所以，|AB|2=．

    由此得到A（x1，y1）、B（x2，y2）两点间的距离公式：．

    根据定义：两点之间线段的长度，叫做这两点之间的距离．

    因此，线段AB的长度计算公式为．

    （问题）

    （1）平面直角坐标系中有两点A（0，1）、B（2，3），求线段AB的长；

    （2）表示线段MN的长，其中点M的坐标为（a，b），点N的坐标为______；

    （3）如图，在x轴上有一点P（x，0），试求PA+PB的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知矩形的边长．某一时刻，动点从点出发沿方向以的速度向点匀速运动；同时，动点从点出发沿方向以的速度向点匀速运动，问：

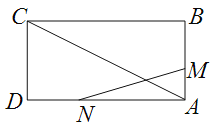
    （1）经过多少时间，的面积等于矩形面积的？

    （2）是否存在时刻t，使以A,M,N为顶点的三角形与相似？若存在，求t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用，表示直角三角形的两直角边（），下列四个说法：

    ①，②，③，④.

    其中说法正确的是 …………………………………………………………（ ）

    A. ①② B. ①②③ C. ①②④ D. ①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,在AC上,甲的速度是乙的速度的1.5倍,设t分后甲、乙两遥控车与B处的距离分别为d1,d2(单位:米),则d1,d2与t的函数关系如图,试根据图象解决下列问题.

    （1）填空：乙的速度v2=________米/分;

    （2）写出d1与t的函数表达式;

    （3）若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探究什么时间两遥控车的信号不会产生相互干扰?

    查看答案和解析>>

    同步练习册答案