
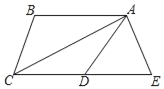
【题目】如图,AC平分∠BAD,∠DCA=∠CAD,在CD的延长线上截取DE=DA,连接AE.
(1)求证:AB∥CD;
(2)若AE=5,AC=12,求线段CE的长;
(3)在(2)的条件下,若线段CD上有一点P,使△DPA的面积是△ACD面积的六分之一,求PC长.
【答案】(1)证明见解析(2)13(3)![]()
【解析】
(1)由AC平分∠BAD,得到∠BAC=∠DAC,等量代换得到∠BAC=∠ACD,根据平行线的判定定理即可得到结论;
(2)根据等腰三角形的性质得到∠DAE=∠E,根据三角形的内角和得到∠CAE=90°,根据勾股定理得到CE=![]() =
=![]() =13;
=13;
(3)根据三角形的面积公式即可得到结论.
(1)∵AC平分∠BAD,
∴∠BAC=∠DAC,
∵∠DCA=∠CAD,
∴∠BAC=∠ACD,
∴AB∥CD;
(2)∵DE=DA,
∴∠DAE=∠E,
∴∠ACD+∠E=∠CAD+∠DAE=![]() ×180°=90°,
×180°=90°,
∴∠CAE=90°,
∴CE=![]() =
=![]() =13;
=13;
(3)∵AD=CD=DE=![]() ,
,
∵点P在线段CD上,△DPA的面积是△ACD面积的六分之一,
∴PD:CD=![]() ,
,
∴![]() =
=![]() ,
,
∴PC=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,△ABC的两条外角平分线AP、CP相交于点P,PH⊥AC于H.若∠ABC=60°,则下面的结论:①∠ABP=30°;②∠APC=60°;③△ABC≌△APC;④PA∥BC;⑤∠APH=∠BPC,其中正确结论的个数是( )
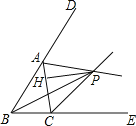
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y= ![]() (x>0)相交于P(1,m).
(x>0)相交于P(1,m). 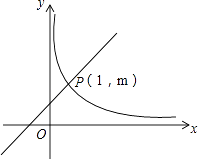
(1)求k的值;
(2)若点Q与点P关于y=x成轴对称,求点Q的坐标为
(3)若过P、Q两点的抛物线与y轴的交点为N(0, ![]() ),求该抛物线的解析式,并求出抛物线的对称轴方程.
),求该抛物线的解析式,并求出抛物线的对称轴方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
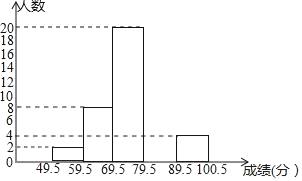
【题目】某校数学兴趣小组成员刘明对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析(每个人的成绩各不相同),绘制成如下下频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题:
(1)频数、频率分布表中a= ,b= ,c= ;
(2)补全频数分布直方图;
(3)如果要画该班上学期期末考试数学成绩的扇形统计图,那么分数在69.5﹣79.5之间的扇形圆心角的度数是 ;
(4)张亮同学成绩为79分,他说:“我们班上比我成绩高的人还有![]() ,我要继续努力.”他的说法正确吗?请说明理由.
,我要继续努力.”他的说法正确吗?请说明理由.
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
频数 | 2 | 8 | 20 | a | 4 | c |
频率 | 0.04 | b | 0.40 | 0.32 | 0.08 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个小组攀登一座450m高的山,第二组的攀登速度是第一组的a倍.
(1)若两个小组同时开始攀登,当a=1.2时,第二组比第一组早15min到达顶峰,求两个小组的攀登速度;
(2)元旦假期这两个小组去攀登另一座hm高的山,第二组比第一组晚出发30min,结果两组同时到达顶峰,问第二组的平均攀登速度比第一组快多少?(用含a,h的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A,B,C三点的坐标分别为(﹣6,7),(﹣3,0),(0,3).
(1)画出三角形ABC,并求三角形ABC的面积;
(2)将三角形ABC平移得到三角形A′B′C′,点C经过平移后的对应点为C′(5,4),画出平移后的三角形A′B′C′,并写出点A′,B′的坐标:A′(________),B′(________)
(3)已知点P(﹣3,m)为三角形ABC内一点,将点P向右平移4个单位后,再向下平移6个单位得到点Q(n,﹣3),则m=________,n=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以点A和点B为圆心,大于![]() AB 的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为16,△ABC的周长28,则AB为___________.
AB 的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为16,△ABC的周长28,则AB为___________.
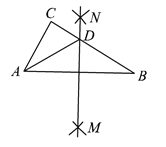
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=8cm,∠BPC=118°,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是_____cm,∠DPE=_____°.
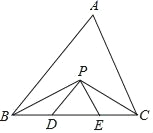
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com