
分析 连接AC,将△BPC顺时针旋转60°至△BEF,作出相应辅助线,让条件集中;要使PA+PB+PC最小只要AP,PE,EF在同一直线上,从而求得PA+PB+PC的最小值.
解答 解:如图所示,P是矩形ABCD对角线BD上一点
将△BPC顺时针旋转60°至△BEF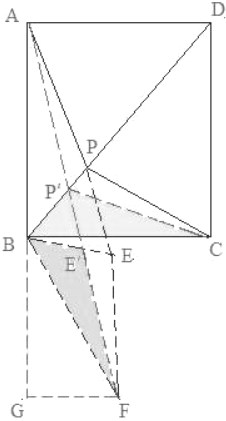
则PC=EF;BE=PB;∠PBE=60°
∴△PBE是等边三角形
∴PB=PE
∴PA+PB+PC=PA+PE+EF
∴要使PA+PB+PC最小只要AP,PE,EF在同一直线上,
如图:可得最小P′A+P′B+P′C=AP′+P′E′+E′F=AF.
作FG⊥AB延长线于G
∴∠CBF=∠P′BE′=60°
∴∠ABF=90°+60°=150°;∴∠GBF=30°
∵△P′BC≌△E′BF
∴BF=BC=$\sqrt{3}$
∴BG=BF•cos30°=$\sqrt{3}×\frac{\sqrt{3}}{2}$=$\frac{3}{2}$;GF=BF•sin30°=$\sqrt{3}×\frac{1}{2}$=$\frac{\sqrt{3}}{2}$
∴AG=AB+BG=2+$\frac{3}{2}$=$\frac{7}{2}$
∴AF=$\sqrt{A{G}^{2}+G{F}^{2}}$=$\sqrt{13}$
∴PA+PB+PC的最小值为$\sqrt{13}$
点评 本题考查了最短路线问题,巧用旋转,作出辅助线是解题的关键,难度较大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
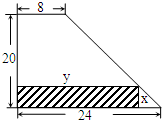 某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,现要从这些边角料上截取矩形铁片(图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x、y应为( )
某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,现要从这些边角料上截取矩形铁片(图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x、y应为( )| A. | x=15,y=12 | B. | x=12,y=15 | C. | x=14,y=10 | D. | x=10,y=14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
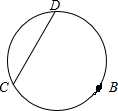 如图,已知CD是圆中的弦,B为圆上一点,且$\widehat{BC}$=$\widehat{BD}$.
如图,已知CD是圆中的弦,B为圆上一点,且$\widehat{BC}$=$\widehat{BD}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com