
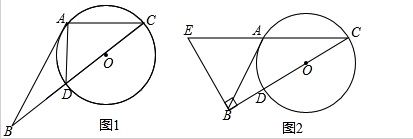
| 5 |
| 3 |
| 2 |
| 5 |
| 2 |
| ||
| 2 |

| AD2+AC2 |
| 5 |
| AD |
| CD |
| 1 | ||
|
| ||
| 5 |
| ||
| 5 |
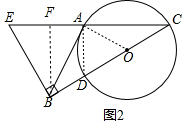
| CD |
| BD |
| CA |
| AF |
| 2r |
| BD |
| 4 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| OB2-OA2 |
| ||
| 2 |
| OA |
| AB |
2
| ||
| 21 |
2
| ||
| 21 |


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
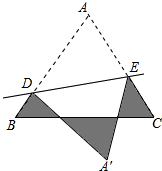 如图,等边三角形ABC的边长为1cm,DE分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分的周长为( )
如图,等边三角形ABC的边长为1cm,DE分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分的周长为( )| A、2cm | B、2.5cm |
| C、3cm | D、3.5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| a |
| 2 |
| a |
| a2 |
| a-1 |
| a2-2a+1 |
| a2-1 |
| a+1 |
| a2-a |
查看答案和解析>>
科目:初中数学 来源: 题型:
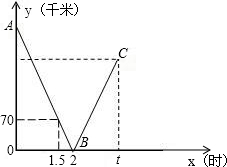 一辆快车和一辆慢车分别从甲、乙两地出发,匀速相向而行,相遇后继续前行,已知两车相遇时快车比慢车多行驶40千米,设行驶的路程为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.
一辆快车和一辆慢车分别从甲、乙两地出发,匀速相向而行,相遇后继续前行,已知两车相遇时快车比慢车多行驶40千米,设行驶的路程为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:
| 6 |
| 7 |
| 4 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com