
【题目】如图,在△ABC中,∠B=90°,点D为边AC的中点,请按下列要求作图
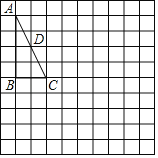
并解决问题:
(1)作点D关于BC的对称点O;
(2)在(1)的条件下,将△ABC绕点O顺时针旋转90°,
①画出旋转后的△EFG(其中A、B、C三点旋转后的对应点分别是点E、F、G);
②若∠C=a,则∠BGC= .(用含a的式子表示)
【答案】(1)见解析;(2)①见解析;②90°﹣α
【解析】
(1)利用网格特点和轴对称的性质画出O点;
(2)①利用网格特点和旋转的性质分别画出A、B、C三点对应点点E、F、G即可;
②先确定∠OCB=∠DCB=α,再利用OB=OC和三角形内角和得到∠BOC=180°﹣2α,根据旋转的性质得到∠COG=90°,则∠BOG=270°﹣2α,于是可计算出∠OGB=α﹣45°,然后计算∠OGC﹣∠OGB即可.
解:(1)如图,点O为所作;
(2)①如图,△EFG为所作;
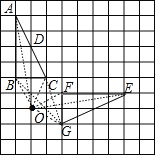
②∵点O与点D关于BC对称,
∴∠OCB=∠DCB=α,
∵OB=OC,
∴∠OBC=∠OCB=α,
∴∠BOC=180°﹣2α,
∵∠COG=90°,
∴∠BOG=180°﹣2α+90°=270°﹣2α,
∵OB=OG,
∴∠OGB=![]() [180°﹣(270°﹣2α)]=α﹣45°,
[180°﹣(270°﹣2α)]=α﹣45°,
∴∠BGC=∠OGC﹣∠OGB=45°﹣(α﹣45°)=90°﹣α.
故答案为90°﹣α.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=6,以A、D为圆心,半径分别为2和1画圆,E、F分别是⊙A、⊙D上的一动点,P是BC上的一动点,则PE+PF的最小值是( )
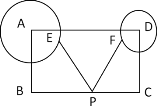
A.5B.6C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
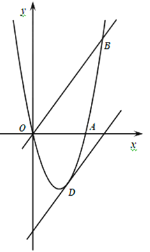
【题目】如图:已知抛物线y=ax2+bx(a≠0)经过A(3,0),B(4,4)两点.
(1)求抛物线解析式.
(2)将直线OB向下平移m个单位后,得到的直线与抛物线只有一个公共点D,求m值及交点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级孟老师数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:
售价x(元/件) | 130 | 150 | 180 |
月销售量y(件) | 210 | 150 | 60 |
月销售利润w(元) | 10500 | 10500 | 6000 |
注:月销售利润=月销售量×(售价﹣进价)
(1)①求y关于x的函数解析式(不要求写出自变量的取值范围);
②运动服的进价是 元/件;当售价是 元/件时,月销利润最大,最大利润是 元.
(2)由于某种原因,该商品进价降低了m元/件(m>0),商家规定该运动服售价不得低于150元/件,该商店在今后的售价中,月销售量与售价仍满足(1)中的函数关系式,若月销售量最大利润是12000元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c图象经过(0,0)、(1,1)、(1,9)三点,下列性质错误的是( )
A.开口向上B.对称轴在y轴左侧
C.经过第四象限D.当x>0,y随x增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三个函数,对于同一个自变量x,对应的函数值分别为![]() ,若恰好有
,若恰好有![]() ,则称y为
,则称y为![]() 的“中值函数”.
的“中值函数”.
(1)若![]() 的图像为直线,
的图像为直线,![]() 的图像是抛物线,则它们的中值函数的图像为( )
的图像是抛物线,则它们的中值函数的图像为( )
A.直线 B.抛物线 C.双曲线 D.以上答案均错
(2)若![]() 、它们的中值函数为
、它们的中值函数为![]() ,
,
①若点P在![]() 、
、![]() 和它们的中值函数图像上,则点P的坐标为_________.
和它们的中值函数图像上,则点P的坐标为_________.
②在如图中,画出上述中值函数的大致图象.并根据图象写出这个中值函数的两条性质;
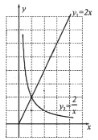
性质1:_______________________________;
性质2:_______________________________;
③利用中值函数的性质说明:面积为1的长方形,当该长方形长与宽相等时,周长最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一颗质地均匀的骰子已连续抛投了2015次,其中抛掷出5点的次数最少,则第2016次一定抛掷出5点
B.某种彩票中奖的概率是1%,因此买100张该种彩票一定会中奖
C.天气预报说明天下雨的概率是![]() ,所以明天将有一半时间在下雨
,所以明天将有一半时间在下雨
D.在同一年出生的367名学生中,至少有两人的生日是同一天
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com