
����Ŀ�����꼶����ʦ��ѧС�龭���г����飬�õ�ij���˶�����������y���������ۼ�x��Ԫ/������һ�κ��������ۼۡ���������������������w��Ԫ���������Ӧֵ���±���
�ۼ�x��Ԫ/���� | 130 | 150 | 180 |
��������y������ | 210 | 150 | 60 |
����������w��Ԫ�� | 10500 | 10500 | 6000 |
ע�������������������������ۼ۩����ۣ�
��1������y����x�ĺ�������ʽ����Ҫ��д���Ա�����ȡֵ��Χ����
���˶����Ľ������� Ԫ/�������ۼ����� Ԫ/��ʱ������������������������ Ԫ��
��2������ij��ԭ����Ʒ���۽�����mԪ/����m��0�����̼ҹ涨���˶����ۼ۲��õ���150Ԫ/�������̵��ڽ����ۼ��У������������ۼ������㣨1���еĺ�����ϵʽ���������������������12000Ԫ����m��ֵ��
���𰸡���1����y����3x+600���ڵ��ۼ���140Ԫʱ����������������������Ϊ10800Ԫ����2��m��ֵΪ10��
��������
��1����y����x�ĺ�������ʽΪ��y��kx+b��k��0�����������������ݵö�Ԫһ�η����飬���k��b��ֵ�ٴ���y��kx+b���ɣ�
��2���˶����Ľ��۵����ۼۼ�ȥÿ����������ÿ��������������������������������ù���x�Ķ��κ������䷽�����ݶ��κ��������ʿɵô𰸣�
��3�����ݽ��۱䶯��ÿ���������Ϊ[x����80��m��]Ԫ��������������������õ�����x�Ķ��κ�������öԳ��ᣬ�ж϶Գ���С��150���ɿ������µĶ��κ��������ʿ�֪����x��150ʱwȡ�����ֵ12000�������m�ķ��̼��ɣ�
��1������y����x�ĺ�������ʽΪ��y��kx+b��k��0��
������ã�![]() ��
��
��ã�![]() ��
��
��y����x�ĺ�������ʽΪy����3x+600��
���˶����Ľ����ǣ�130��10500��210��80��Ԫ����
����������w����x��80������3x+600����
����3x2+840x��48000��
����3��x��140��2+10800��
�൱�ۼ���140Ԫʱ����������������������Ϊ10800Ԫ��
��2��������ã�w��[x����80��m��]����3x+600������3x2+��840��3m��x��48000+600m��
�Գ���Ϊx��140��![]() ��
��
��m��0��
��140��![]() ��140��150��
��140��150��
���̼ҹ涨���˶����ۼ۲��õ���150Ԫ/����
���ɶ��κ��������ʣ���֪��x��150ʱ�������������������12000Ԫ��
�ੁ3��1502+��840��3m����150��48000+600m��12000��
��ã�m��10��
��m��ֵΪ10��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
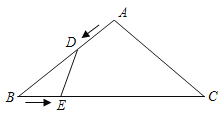
����Ŀ����ͼ��ʾ���ڵ�����ABC�У�AB��AC��10cm��BC��16cm����D�ɵ�A������AB�������B�����˶���ͬʱ��E�ɵ�B������BC�������C�����˶������ǵ��ٶȾ�Ϊ1cm/s������DE�����˶�ʱ��Ϊt��s����0��t��10��������������⣺
��1����tΪ��ֵʱ����BDE�����Ϊ7.5cm2��
��2���ڵ�D��E���˶��У��Ƿ����ʱ��t��ʹ�á�BDE���ABC���ƣ������ڣ��������Ӧ��ʱ��t���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⱳ������ͼ�������ı���ADBC�У���ACB����ADB��90����AD��BD��̽���߶�AC��BC��CD֮���������ϵ.
С��ͬѧ̽���������˼·�ǣ�����BCD�Ƶ�D��ʱ����ת90�㵽��AED������B��C�ֱ����ڵ�A��E������ͼ��������֤��C��A��E��ͬһ��ֱ���ϣ�������CDE�ǵ���ֱ�������Σ�����CE��![]() CD���Ӷ��ó����ۣ�AC+BC��
CD���Ӷ��ó����ۣ�AC+BC��![]() CD.
CD.




�� ͼ�١����� ����ͼ���������������� ͼ�� ͼ��
��Ӧ�ã�
��1����ͼ���У���AC��![]() ��BC��2
��BC��2![]() ����CD�� .
����CD�� .
��2����ͼ����AB����O��ֱ������C��D�ڡ�O������AD����BD����AB��13��BC��12����CD�ij�.
��չ���죺
��3����ͼ������ACB����ADB��90����AD��BD����AC��m��BC��n��m<n������CD�ij����ú�m��n�Ĵ���ʽ��ʾ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶��1�������С�����ñ�˲���ѧУ��˵ĸ߶ȣ���֪��˸߶�CD��3m���������˵�ˮƽ����BD��15m���˵��۾������ĸ߶�EF��1.6m��������CD��ˮƽ����DF��2m�������AB�ĸ߶ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�Ķ��κ���y��x2+bx+b2��b��x��b+3��Χ�ڣ�����ֵ����Сֵ21����b��ֵ�ǣ�������
A.![]() ��2
��2![]() B.
B.![]() ����2
����2![]() C.��4��
C.��4��![]() D.1��4��
D.1��4��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���B��90������DΪ��AC���е㣬�밴����Ҫ����ͼ
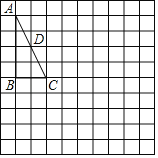
��������⣺
��1������D����BC�ĶԳƵ�O��
��2���ڣ�1���������£�����ABC�Ƶ�O˳ʱ����ת90����
�ٻ�����ת�����EFG������A��B��C������ת��Ķ�Ӧ��ֱ��ǵ�E��F��G����
������C��a�����BGC���� �������ú�a��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
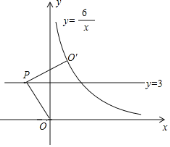
����Ŀ����ͼ����P��ֱ��y��3�ϵĶ��㣬����PO����PO��P����ת90����PO��������O���պ�����˫����![]() ��x��0����ʱ����P�ĺ��������п���ֵΪ_____��
��x��0����ʱ����P�ĺ��������п���ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
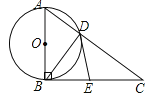
����Ŀ����ͼ����֪Rt��ABC����ABC=90������ֱ�DZ�ABΪֱ������O����б��AC�ڵ�D������BD��
��1����AD=3��BD=4�����BC�ij���
��2��ȡBC���е�E������ED����֤����ED���O���У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
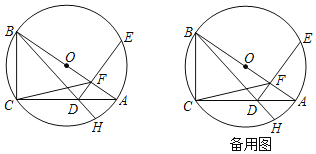
����Ŀ����ͼ��![]() ��
��![]() ���ڽ������Σ�ABΪ
���ڽ������Σ�ABΪ![]() ֱ����
ֱ����![]() ��
��![]() ����DΪ�߶�AC��һ���㣬����D��AB�Ĵ��߽�
����DΪ�߶�AC��һ���㣬����D��AB�Ĵ��߽�![]() �ڵ�E����AB�ڵ�F������BD��CF�����ӳ�BD��
�ڵ�E����AB�ڵ�F������BD��CF�����ӳ�BD��![]() �ڵ�H��
�ڵ�H��
![]() ��
��![]() �İ뾶��
�İ뾶��
![]() ��DE����Բ��Oʱ����AD�ij���
��DE����Բ��Oʱ����AD�ij���
![]() ��֤��
��֤��![]() ��
��
![]() ��
��![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com