
【题目】九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交线段AB于点D;以点A为圆心,AD长为半径画弧,交线段AC于点E,连结CD.

(1)若∠A=28°,求∠ACD的度数.
(2)设BC=a,AC=b.
①线段AD的长是方程x2+2ax﹣b2=0的一个根吗?说明理由.
②若AD=EC,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
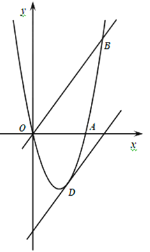
【题目】如图:已知抛物线y=ax2+bx(a≠0)经过A(3,0),B(4,4)两点.
(1)求抛物线解析式.
(2)将直线OB向下平移m个单位后,得到的直线与抛物线只有一个公共点D,求m值及交点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以AC,BC为边作等边△ACD和等边△BCE.设△ACD,△BCE,△ABC的面积分别是S1,S2,S3,现有如下结论:
①S1∶S2=AC2∶BC2;②连接AE,BD,则△BCD≌△ECA;③若AC⊥BC,则S1·S2=![]() S23.
S23.
其中结论正确的序号是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级孟老师数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:
售价x(元/件) | 130 | 150 | 180 |
月销售量y(件) | 210 | 150 | 60 |
月销售利润w(元) | 10500 | 10500 | 6000 |
注:月销售利润=月销售量×(售价﹣进价)
(1)①求y关于x的函数解析式(不要求写出自变量的取值范围);
②运动服的进价是 元/件;当售价是 元/件时,月销利润最大,最大利润是 元.
(2)由于某种原因,该商品进价降低了m元/件(m>0),商家规定该运动服售价不得低于150元/件,该商店在今后的售价中,月销售量与售价仍满足(1)中的函数关系式,若月销售量最大利润是12000元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三个函数,对于同一个自变量x,对应的函数值分别为![]() ,若恰好有
,若恰好有![]() ,则称y为
,则称y为![]() 的“中值函数”.
的“中值函数”.
(1)若![]() 的图像为直线,
的图像为直线,![]() 的图像是抛物线,则它们的中值函数的图像为( )
的图像是抛物线,则它们的中值函数的图像为( )
A.直线 B.抛物线 C.双曲线 D.以上答案均错
(2)若![]() 、它们的中值函数为
、它们的中值函数为![]() ,
,
①若点P在![]() 、
、![]() 和它们的中值函数图像上,则点P的坐标为_________.
和它们的中值函数图像上,则点P的坐标为_________.
②在如图中,画出上述中值函数的大致图象.并根据图象写出这个中值函数的两条性质;
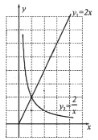
性质1:_______________________________;
性质2:_______________________________;
③利用中值函数的性质说明:面积为1的长方形,当该长方形长与宽相等时,周长最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤4元的价格购进某种水果若干斤,然后以每斤6元的价格出售,每天可售出150斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出30斤,为保证每天至少售出360斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利450元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com