
����Ŀ������������������ͬһ���Ա���x����Ӧ�ĺ���ֵ�ֱ�Ϊ![]() ����ǡ����
����ǡ����![]() �����yΪ
�����yΪ![]() ������ֵ������.
������ֵ������.
��1����![]() ��ͼ��Ϊֱ�ߣ�
��ͼ��Ϊֱ�ߣ�![]() ��ͼ���������ߣ������ǵ���ֵ������ͼ��Ϊ�� ��
��ͼ���������ߣ������ǵ���ֵ������ͼ��Ϊ�� ��
A.ֱ�� B.������ C.˫���� D.���ϴ𰸾���
��2����![]() �����ǵ���ֵ����Ϊ
�����ǵ���ֵ����Ϊ![]() ��
��
������P��![]() ��
��![]() �����ǵ���ֵ����ͼ���ϣ����P������Ϊ_________.
�����ǵ���ֵ����ͼ���ϣ����P������Ϊ_________.
������ͼ�У�����������ֵ�����Ĵ���ͼ��.������ͼ��д�������ֵ�������������ʣ�
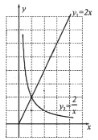
����1��_______________________________��
����2��_______________________________��
��������ֵ����������˵�������Ϊ1�ij����Σ����ó����γ�������ʱ���ܳ���С.
���𰸡���1��B����2���٣�1��2����������1����x=1ʱ����ֵ����y��ֵ��СΪ2��
����2����0<x<1ʱ����ֵ����y��x���������С���ۼ����
��������
��1������������![]() �������
�������![]() ���ж�y�ĺ���ͼ��
���ж�y�ĺ���ͼ��
��2���ٸ��ݵ�P��![]() ��
��![]() �����ǵ���ֵ����ͼ���ϣ��������̼��������P�����ꣻ�ڸ�����ֵ��������ʽ��������ͼ����ͼ��۲켴�ɵó����ʼ��ɣ����賤Ϊx�����Ϊ
�����ǵ���ֵ����ͼ���ϣ��������̼��������P�����ꣻ�ڸ�����ֵ��������ʽ��������ͼ����ͼ��۲켴�ɵó����ʼ��ɣ����賤Ϊx�����Ϊ![]() �����ܳ�
�����ܳ�![]() ��������ֵ�������ʼ������.
��������ֵ�������ʼ������.
�⣺��1����������![]()
��![]()
![]()
��y��Ȼ�Ƕ��κ�������ֵ������ͼ��Ϊ������
��ѡB��
��2����![]() ��P��
��P��![]() ��
��![]() �����ǵ���ֵ����ͼ����
�����ǵ���ֵ����ͼ����
��![]() ���
���![]()
��![]()
���P��������1��2����
�ڸ��ݺ�������ʽ������ͼ�����£�

����1����x=1ʱ����ֵ����y��ֵ��СΪ2��
����2����0<x<1ʱ����ֵ����y��x���������С��
��3���賤Ϊx�����Ϊ![]() �����ܳ�
�����ܳ�![]()
����ֵ�����Ķ����֪��cΪ![]() ����ֵ����
����ֵ����
�����ʿ�֪����![]() ��
��![]() ʱ��cȡ����Сֵ
ʱ��cȡ����Сֵ
��![]()
��![]() ��-1��ȥ��
��-1��ȥ��
���ij�����Ϊ������ʱ���ܳ���С.


 53������ϵ�д�
53������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
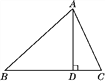
����Ŀ����ͼ������ABC�У�AD��BC���ϵĸߣ�tanB��cos��DAC.
��1����֤��AC��BD��
��2����sin C��![]() ��BC��12������ABC�������
��BC��12������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶��1�������С�����ñ�˲���ѧУ��˵ĸ߶ȣ���֪��˸߶�CD��3m���������˵�ˮƽ����BD��15m���˵��۾������ĸ߶�EF��1.6m��������CD��ˮƽ����DF��2m�������AB�ĸ߶ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���B��90������DΪ��AC���е㣬�밴����Ҫ����ͼ
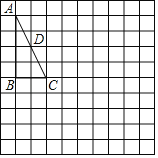
��������⣺
��1������D����BC�ĶԳƵ�O��
��2���ڣ�1���������£�����ABC�Ƶ�O˳ʱ����ת90����
�ٻ�����ת�����EFG������A��B��C������ת��Ķ�Ӧ��ֱ��ǵ�E��F��G����
������C��a�����BGC���� �������ú�a��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
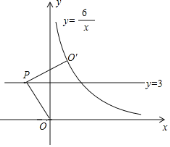
����Ŀ����ͼ����P��ֱ��y��3�ϵĶ��㣬����PO����PO��P����ת90����PO��������O���պ�����˫����![]() ��x��0����ʱ����P�ĺ��������п���ֵΪ_____��
��x��0����ʱ����P�ĺ��������п���ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC��ֱ������ϵ�ڣ��������������ֱ�ΪA��0��3����B��3��4����C��2��2����������������ÿ��С�����εı߳���Ϊһ����λ���ȣ���

�ٻ�����ABC����ƽ��4����λ���ȵõ�����A1B1C1 �� ��C1��������________��
���Ե�BΪλ�����ģ��������ڻ�����A2B2C2 �� ʹ��A2B2C2����ABCλ�ƣ���λ�Ʊ�Ϊ2��1����C2��������________��
����M��a��b��Ϊ�߶�AC����һ�㣬д����M�Ķ�Ӧ��M2������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
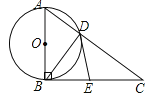
����Ŀ����ͼ����֪Rt��ABC����ABC=90������ֱ�DZ�ABΪֱ������O����б��AC�ڵ�D������BD��
��1����AD=3��BD=4�����BC�ij���
��2��ȡBC���е�E������ED����֤����ED���O���У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
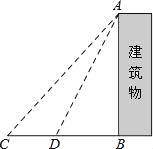
����Ŀ��ij��ѧ���꼶��ѧ��ȤС�������������AB�ĸ߶ȣ�������C�����������ﶥ�ˣ��������Ϊ48��������������ķ���ǰ��6����D�����������Ϊ64����������ĸ߶ȣ���������ĸ߶Ⱥ��Բ��ƣ������ȷ��0.1�ף�
���ο����ݣ�sin48���![]() ��tan48���
��tan48���![]() ��sin64���
��sin64���![]() ��tan64���2��
��tan64���2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
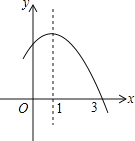
����Ŀ����֪���κ���y����x2+2x+m�IJ���ͼ����ͼ��ʾ�������x��һԪ���η��̩�x2+2x+m��0�Ľ�Ϊ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com