
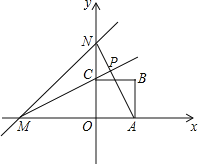
【题目】直线y=x+8分别与x轴、y轴相交于点M,N,边长为4的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交于点P,若正方形绕着点O旋转一周,则PC长度的最小值是_____.
【答案】4![]() ﹣4.
﹣4.
【解析】
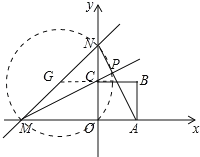
首先证明△MOC≌△NOA,推出∠MPN=90°,推出P在以MN为直径的圆上,所以当圆心G,点P,C三点共线时,PC长度的最小值.求出此时的PC即可.
在△MOC和△NOA中,
∵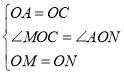 ,∴△MOC≌△NOA(SAS),∴∠CMO=∠ANO.
,∴△MOC≌△NOA(SAS),∴∠CMO=∠ANO.
∵∠CMO+∠MCO=90°,∠MCO=∠NCP,
∴∠NCP+∠CNP=90°,
∴∠MPN=90°,
∴MP⊥NP.
在正方形旋转的过程中,同理可证,∴∠CMO=∠ANO,可得∠MPN=90°,MP⊥NP,
∴P在以MN为直径的圆上.
∵直线y=x+8分别与x轴、y轴相交于点M,N,
∴M(﹣8,0),N(0,8),
∴圆心G为(﹣4,4),半径为4![]() ,
,
∵PG﹣GC≤PC,
∴当圆心G,点P,点C三点共线时,PC最小.
∵GN=GM,CN=CO=4,∴GC![]() OM=4,
OM=4,
这个最小值为GP﹣GC=4![]() 4.
4.
故答案为:4![]() 4.
4.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-4x+3.
(1)用配方法求其图象的顶点C的坐标,并描述该函数的函数值随自变量的增减而变化的情况;
(2)求函数图象与x轴的交点A,B的坐标,及△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”共享单车已经成了很多人出行的主要选择.
(1)考虑到共享单车市场竞争激烈,摩拜公司准备用不超过60000元的资金再购进A,B两种规格的自行车100辆,且A型车不超过60辆.已知A型的进价为500元/辆,B型车进价为700元/辆,设购进A型车m辆,求出m的取值范围;
(2)已知A型车每月产生的利润是100元/辆,B型车每月产生的利润是90元/辆,在(1)的条件下,求公司每月的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
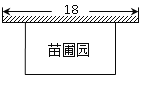
【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论 ①a+b+c<0②a﹣b+c<0③b+2a<0④abc>0⑤b2<4ac,其中正确的个数是( )
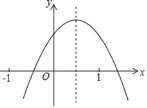
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,
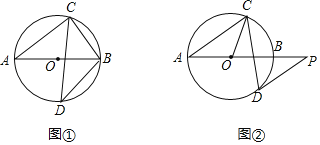
(1)如图①,若D为弧AB的中点,求∠ABC和∠ABD的大小;
(2)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:
类比是数学中常用的数学思想.比如,我们可以类比多位数的加、减、乘、除的竖式运算方法,得到多项式与多项式的加、减、乘、除的运算方法.

理解应用:
(1)请仿照上面的竖式方法计算:![]() ;
;
(2)已知两个多项式的和为![]() ,其中一个多项式为
,其中一个多项式为![]() .请用竖式的方法求出另一个多项式.
.请用竖式的方法求出另一个多项式.
(3)已知一个长为![]() ,宽为
,宽为![]() 的矩形
的矩形![]() ,将它的长增加8.宽增加
,将它的长增加8.宽增加![]() 得到一个新矩形
得到一个新矩形![]() ,且矩形
,且矩形![]() 的周长是
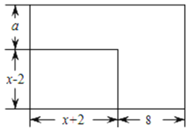
的周长是![]() 周长的3倍(如图).同时,矩形
周长的3倍(如图).同时,矩形![]() 的面积和另一个一边长为
的面积和另一个一边长为![]() 的矩形
的矩形![]() 的面积相等,求
的面积相等,求![]() 的值和矩形
的值和矩形![]() 的另一边长.
的另一边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)![]()
(2)![]()
(3)(6x-1)2-25=0
(4)![]()
(5) ![]()
(6) ![]()
(7)![]() +
+![]() +(﹣1)0﹣2sin45°
+(﹣1)0﹣2sin45°
(8)6tan230°-cos30°·tan60°-2sin 45°+cos60°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com