
【题目】某班举行了“庆祝建党98周年知识竞赛”活动,班长安排张小明购买奖品,如图两幅图是张小明买回奖品时与班长的对话情况:

请根据图1、图2的信息,解答下列问题:
(1)张小明买了两种笔记本各多少本?(要求列一元一次方程解决问题)
(2)为什么班长说不可能找回68元钱,请说明理由。
【答案】(1)张小明买了5元的笔记本25本,8元的笔记本15本;(2)见解析.
【解析】
(1)设5元、8元的笔记本分别买x本、y本,根据题意列出关于x、y的二元一次方程组,求出x、y的值即可;
(2)根据(1)中求出的5元、8元的笔记本的本数求出应找回的钱数,再与68相比较即可得出结论.
解:(1)设张小明买了第一种笔记本x本,
5x+8(40-x)=300-(68-13),解得x=25;
则40-x=15(本).
答:张小明买了5元的笔记本25本,8元的笔记本15本;
(2)设买m本5元的笔记本,则买(40-m)本8元的笔记本,
依题意得,5m+8(40-m)=300-68,
解得:m=![]() ,
,
∵m是正整数,
∴m=![]() 不合题意,舍去.
不合题意,舍去.
∴不能找回68元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
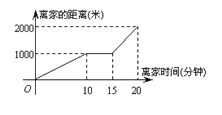
【题目】某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,如图所示是小明从家到学校这一过程中所走的路程 s(米)与时间 t(分)之间的关系.
(1)小明从家到学校的路程共 米,从家出发到学校,小明共用了 分钟;
(2)小明修车用了多长时间?
(3)小明修车以前和修车后的平均速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,垂足为
,垂足为![]() .
.
(1)如图,连接![]() 、
、![]() .求证四边形
.求证四边形![]() 为菱形,并求
为菱形,并求![]() 的长;
的长;
(2)如图,动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时出发,沿
两点同时出发,沿![]() 和
和![]() 各边匀速运动一周.即点
各边匀速运动一周.即点![]() 自
自![]() →
→![]() →
→![]() →
→![]() 停止,点
停止,点![]() 自
自![]() →
→![]() →
→![]() →
→![]() 停止.在运动过程中,
停止.在运动过程中,
①已知点![]() 的速度为每秒5
的速度为每秒5![]() ,点
,点![]() 的速度为每秒4
的速度为每秒4![]() ,运动时间为
,运动时间为![]() 秒,当
秒,当![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形时,求
四点为顶点的四边形是平行四边形时,求![]() 的值.
的值.
②若点![]() 、
、![]() 的运动路程分别为
的运动路程分别为![]() 、
、![]() (单位:
(单位:![]() ,
,![]() ),已知
),已知![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形,写出
四点为顶点的四边形是平行四边形,写出![]() 与
与![]() 满足的数量关系式.(直接写出答案,不要求证明)
满足的数量关系式.(直接写出答案,不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c是![]() 的三边,且满足
的三边,且满足![]() ,试判断
,试判断![]() 的形状.
的形状.
阅读下面解题过程:
解:由![]() 得:
得:![]() ①
①
![]() ②
②
即![]() ③
③
∴![]() 为Rt△.④
为Rt△.④
试问:以上解题过程是否正确:_________.
若不正确,请指出错在哪步?______(填代号)
错误原因是______________________.
本题的结论应为_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D为△ABC边BC的延长线上一点.∠ABC的角平分线与∠ACD的角平分线交于点M,将△MBC以直线BC为对称轴翻折得到△NBC,∠NBC的角平分线与∠NCB的角平分线交于点Q,若∠A=48°,则∠BQC的度数为( )
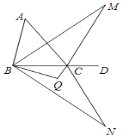
A. 138° B. 114° C. 102° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图的统计图(图中信息不完整).已知A,B两组捐款人数的比为1∶5.
捐款人数分组统计表
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | |
D | 30≤x<40 | |
E | x≥40 |
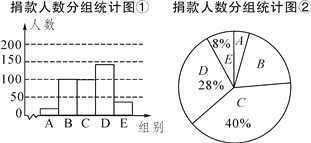
请结合以上信息解答下列问题:
(1)a=____,本次调查的样本容量是______;
(2)先求出C组的人数,再补全“捐款人数分组统计图①;
(3)若该学校自愿捐款的学生有1500人,请估计捐款不少于30元的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意写出一个数位不含零的三位数,任取三个数字中的两个,组合成所有可能的两位数(有6个),求出所有这些两位数的和,然后将它除以原三位数的各个数位上的数的和.例如,对三位数223,取其两个数字组成所有可能的两位数:22,23,22,23,32,32.它们的和是154.三位数223各位数的和是7,![]() 再换几个数试一试,你发现了什么?请写出你按上面方法的探索过程和所发现的结果,并运用代数式的知识说明所发现的结果的正确性.
再换几个数试一试,你发现了什么?请写出你按上面方法的探索过程和所发现的结果,并运用代数式的知识说明所发现的结果的正确性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com