
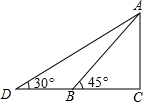
 如图,幼儿园为了加强安全管理,决定将园内的滑滑梯的倾角由45°降为30°,已知原滑滑梯AB的长为5m,点D,B,C在同一水平地面上.
如图,幼儿园为了加强安全管理,决定将园内的滑滑梯的倾角由45°降为30°,已知原滑滑梯AB的长为5m,点D,B,C在同一水平地面上.分析 本题中两个直角三角形有公共的边,那么可利用这条公共直角边进行求解.
(1)求AD长的时候,可在直角三角形ADC内,根据∠D的度数和AC的长,运用正弦函数求出AD的长.
(2)本题实际要求的是BD的长是否超过3m,如果超过了那么这样修改滑板的坡度就不可行,反之,则可行.就要先求出BD的长.根据BD=CD-BC即可求解.
解答 解:(1)Rt△ABC中,AC=AB×sin45°=$\frac{5\sqrt{2}}{2}$(m),
Rt△ADC中,BC=AB×cos45°=$\frac{5\sqrt{2}}{2}$(m),
AD=$\frac{AC}{sin30°}$=5$\sqrt{2}$,
∴AD-AB≈2.07(m). 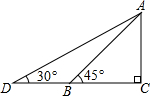
改善后滑滑梯会加长2.07 m;
(2)这样改造能行.
在直角△ACD=$\frac{AC}{tan30°}$=$\frac{5\sqrt{6}}{2}$,
因为CD-BC≈2.59(m),而6-3>2.59.
因此,像这样改造是不可行的.
点评 本题主要考查了解直角三角形的应用,利用这两个直角三角形有公共的直角边求解是解决此类题目的基本出发点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ①②③ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
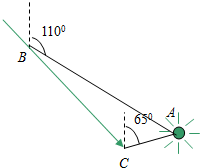 如图,货轮在海上自B点沿方位角(指从北按顺时针转到目标线的角度)140°的方向航行,为了确定船位,船在B点观测灯塔A的方位角为110°,船到达C点,观测灯塔A的方位是65°,求AB与AC的夹角是多少?
如图,货轮在海上自B点沿方位角(指从北按顺时针转到目标线的角度)140°的方向航行,为了确定船位,船在B点观测灯塔A的方位角为110°,船到达C点,观测灯塔A的方位是65°,求AB与AC的夹角是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
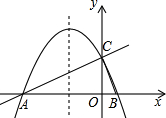 如图,在平面直角坐标系xoy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$,且经过A,C两点,与x轴的另一个交点为点B.
如图,在平面直角坐标系xoy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$,且经过A,C两点,与x轴的另一个交点为点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com