
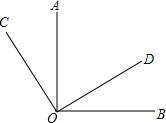
 如图:OA⊥OB,OC⊥OD.
如图:OA⊥OB,OC⊥OD.| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |


科目:初中数学 来源: 题型:
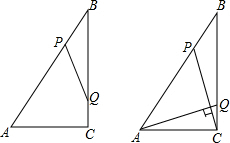 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 10 |
| 1 |
| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
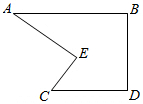 小明到工厂去进行社会实践活动时,发现工人师傅生产了一种如图所示的零件,工人师傅告诉他:AB∥CD,∠BAE=30°,∠AEC=70°,小明马上运用已学的数学知识得出了∠ECD的度数,聪明的你一定知道∠ECD=
小明到工厂去进行社会实践活动时,发现工人师傅生产了一种如图所示的零件,工人师傅告诉他:AB∥CD,∠BAE=30°,∠AEC=70°,小明马上运用已学的数学知识得出了∠ECD的度数,聪明的你一定知道∠ECD=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com