
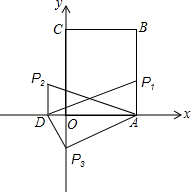
 如图所示平面直角坐标系中,矩形OABC的顶点B的坐标为(4,8),若一次函数y=kx+2的图象平分矩形OABC的面积.
如图所示平面直角坐标系中,矩形OABC的顶点B的坐标为(4,8),若一次函数y=kx+2的图象平分矩形OABC的面积.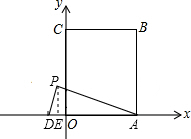
| AE |
| PE |
| PE |
| DE |
| 4-a |
| a+2 |
| a+2 |
| a-(-1) |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |


科目:初中数学 来源: 题型:
| A、由2=3-x,得x=2+3 | ||||
| B、由6y=4,得y=4-6 | ||||
C、由
| ||||
| D、由4-x=2x,得2x-x=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 一辆园林喷灌车和一辆公交车分别从一条笔直公路两端点A、B同时出发匀速行驶,喷灌车中途停车在供水站加满水后继续以原速进行作业到达终点B,公交车到达A处进站检修,之后沿原路原点返回到点B.如图是两车与点A的距离y(千米)与运行时间t(时)的函数图象.
一辆园林喷灌车和一辆公交车分别从一条笔直公路两端点A、B同时出发匀速行驶,喷灌车中途停车在供水站加满水后继续以原速进行作业到达终点B,公交车到达A处进站检修,之后沿原路原点返回到点B.如图是两车与点A的距离y(千米)与运行时间t(时)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
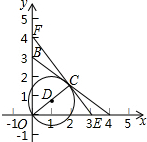 如图,在平面直角坐标系中,点A、B的坐标分别为(a,0),(0,b),且a:b=4:3,点C是AB的中点,以OC为直径作圆D,且圆D的直径为
如图,在平面直角坐标系中,点A、B的坐标分别为(a,0),(0,b),且a:b=4:3,点C是AB的中点,以OC为直径作圆D,且圆D的直径为| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,交AB于点D.
如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
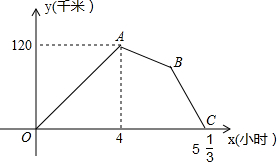 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用50分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用50分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:| 5 |
| 6 |
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com