
分析 首先根据3a-4b=0,判断出b=$\frac{3}{4}$a;然后把b=$\frac{3}{4}$a代入分式$\frac{2ab-{b}^{2}}{{a}^{2}+3{b}^{2}}$,求出它的值是多少即可.
解答 解:∵3a-4b=0,
∴b=$\frac{3}{4}$a,
∴$\frac{2ab-{b}^{2}}{{a}^{2}+3{b}^{2}}$
=$\frac{2a•\frac{3}{4}a{-(\frac{3}{4}a)}^{2}}{{a}^{2}+3{×(\frac{3}{4}a)}^{2}}$
=$\frac{{\frac{15}{16}a}^{2}}{{\frac{43}{16}a}^{2}}$
=$\frac{15}{43}$
即分式$\frac{2ab-{b}^{2}}{{a}^{2}+3{b}^{2}}$的值是$\frac{15}{43}$.
点评 此题主要考查了分式的求值,要熟练掌握,解答时应从已知条件和所求问题的特点出发,进行适当的变形、转化,解答此题的关键是根据3a-4b=0,判断出b=$\frac{3}{4}$a.


科目:初中数学 来源: 题型:选择题
| A. | (1,4) | B. | (-7,0) | C. | (1,0) | D. | (-7,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
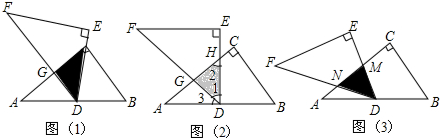
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
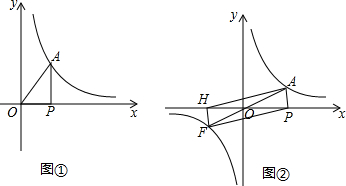
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
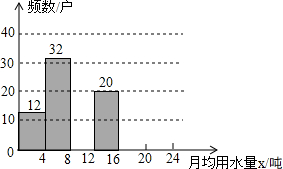 2014年,河北省委宣传部主办“河北节约之星”活动,表彰节水先进典型,省委宣传部号召全社会以节水先进典型为榜样,牢固树立节约用水理念,争做节俭美德的传承者,节约用水的践行者.小鹏想了解某小区住户月均用水情况,随机调查了该小区部分住户,并将调查数据绘制成如图所示的频数分布直方图(不完整)和如下的频数分布表.
2014年,河北省委宣传部主办“河北节约之星”活动,表彰节水先进典型,省委宣传部号召全社会以节水先进典型为榜样,牢固树立节约用水理念,争做节俭美德的传承者,节约用水的践行者.小鹏想了解某小区住户月均用水情况,随机调查了该小区部分住户,并将调查数据绘制成如图所示的频数分布直方图(不完整)和如下的频数分布表.| 月均用水量x(吨) | 频数(户) | 频率 |
| 0<x≤4 | 12 | a |
| 4<x≤8 | 32 | 0.32 |
| 8<x≤12 | b | c |
| 12<x≤16 | 20 | 0.2 |
| 16<x≤20 | 8 | 0.08 |
| 20<x≤24 | 4 | 0.04 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
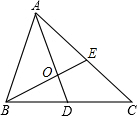 如图,在△ABC中,点O是重心,BC=10,连接AO并延长交BC于点D,连接BO并延长交AC于点E,AD⊥BE.若BE=2OD=6,AO=6,则AC的值为( )
如图,在△ABC中,点O是重心,BC=10,连接AO并延长交BC于点D,连接BO并延长交AC于点E,AD⊥BE.若BE=2OD=6,AO=6,则AC的值为( )| A. | 8 | B. | 4$\sqrt{10}$ | C. | 12 | D. | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com