
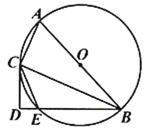
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦,
的弦,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)![]() ________
________![]() (填“>”,“<”或“=”);
(填“>”,“<”或“=”);
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)若![]() 的直径为10,sin∠BAC=
的直径为10,sin∠BAC=![]() ,求
,求![]() 的长.
的长.
【答案】(1)=;(2)见解析;(3)2.8
【解析】
(1)由AB为⊙O的直径,得到∠ACB=90°,求得∠ACB=∠D,根据角平分线的性质得到∠ABC=∠CBD,通过相似三角形得到∠BAC=∠BCD,四边形ABEC是圆内接四边形,得出∠CED=∠BAC,根据余角的性质即可证得∠DCE=∠CBE;
(2)连接OC,由等腰三角形的性质得出∠OBC=∠OCB,等量代换得到∠OCB=∠CBD,证得OC∥BD,即可证得OC⊥CD,即可得到结论;
(3)解Rt△ABC求得BC,进而求得AC,通过三角形相似的性质得出CD=4.8,BD=6.4,进而求得DE=3.6,即可求得BE=2.8.
(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∵CD⊥BE
∠D=90°,
∴∠ACB=∠D,
∵BC是∠ABE的平分线,
∴∠ABC=∠CBD,
∴△ABC∽△CBD,
∴∠BAC=∠BCD,
∵四边形ABEC是圆内接四边形
∴∠CED=∠BAC,
∵∠DBC+∠BCD=90°,∠ECD+∠CED=90°
∴∠DCE=∠CBE;
故答案为=;
(2)证明:连接OC,
∵OB=OC,
∴∠OBC=∠OCB,
∵∠ABC=∠CBD
∴∠OCB=∠CBD,
∴OC∥BD,
∵CD⊥BD,
∴OC⊥CD,
∴CD是⊙O的切线;
(3)∵⊙O的直径为10,sin∠BAC=![]() ,
,
∴sin∠BAC=![]() =
=![]() ,
,
∴BC=8,
∴AC=![]() =6,
=6,
∵△ABC∽△CBD,
∴![]() ,即
,即![]() ,
,
∴CD=4.8,BD=6.4,
∵∠CDE=∠ACB=90°,∠CED=∠BAC,
∴△CED∽△BAC,
∴![]() ,即
,即![]() ,
,
∴DE=3.6,
∴BE=BD﹣DE=6.4﹣3.6=2.8.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
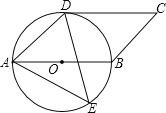
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE=![]() ,求AE的值.
,求AE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C.
(1)求证:四边形ABCD是正方形;
(2)连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段MN、ND、DH之间的数量关系,并说明理由.
(3)若EG=4,GF=6,BM=3![]() ,求AG、MN的长.
,求AG、MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点E和点F是对角线AC上的两点,AF=CE,DF=BE,且DF∥BE,过点C作CG⊥AB交AB延长线与点G.
(1)求证:四边形ABCD是平行四边形;
(2)若tan∠CAB=![]() ,∠CBG=45°,BC=
,∠CBG=45°,BC=![]() ,则ABCD的面积是 .
,则ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“南昌之星”摩天轮,位于江西省南昌市红谷滩新区红角洲赣江边上的赣江市民公园,摩天轮高![]() (最高点到地面的距离).如图,点
(最高点到地面的距离).如图,点![]() 是摩天轮的圆心,
是摩天轮的圆心,![]() 是其垂直于地面的直径,小贤在地面点
是其垂直于地面的直径,小贤在地面点![]() 处利用测角仪测得摩天轮的最高点
处利用测角仪测得摩天轮的最高点![]() 的仰角为
的仰角为![]() ,测得圆心
,测得圆心![]() 的仰角为
的仰角为![]() ,则摩天轮的半径为________
,则摩天轮的半径为________![]() (结果保留
(结果保留![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 、
、![]() 、
、![]() 在第二象限,横坐标分别是-4、-2、-1,双曲线
在第二象限,横坐标分别是-4、-2、-1,双曲线![]() 过
过![]() 、
、![]() 、
、![]() 三点,且
三点,且![]() .
.
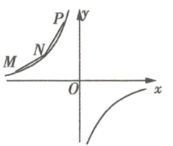
(1)求双曲线的解析式;
(2)过![]() 点的直线
点的直线![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,且
,且![]() ,且交
,且交![]() 于另一点
于另一点![]() ,求
,求![]() 点坐标;
点坐标;
(3)以![]() 为边(顺时针方向)作正方形
为边(顺时针方向)作正方形![]() ,平移正方形使
,平移正方形使![]() 落在
落在![]() 轴上,点
轴上,点![]() 、
、![]() 对应的点
对应的点![]() 、
、![]() 正好落在反比例函数
正好落在反比例函数![]() 上,求
上,求![]() 对应点
对应点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教育主管部门针对中小学生非统考学科的教学情况进行年终考评,抽取某校八年级部分同学的成绩作为样本,把成绩按![]() (优秀)、
(优秀)、![]() (良好)、
(良好)、![]() (及格)、
(及格)、![]() (不及格)四个级别进行统计,并绘成如图所示不完整的条形统计图和扇形统计图.
(不及格)四个级别进行统计,并绘成如图所示不完整的条形统计图和扇形统计图.
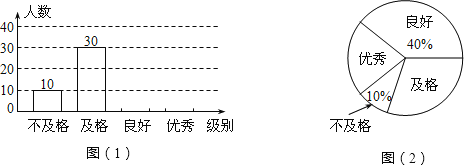
(1)求被抽取的学生人数;
(2)补全条形统计图,并求![]() 的圆心角度数;
的圆心角度数;
(3)该校八年级有![]() 名学生,请估计达到
名学生,请估计达到![]() 、
、![]() 两级的总人数.
两级的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
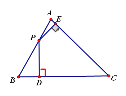
【题目】如图,在△ABC中,∠C=45°,∠B=60°,BC为![]() +1,点P为边AB上一动点,过点P作PD⊥BC于点D,PE⊥AC于点E,则DE的最小值为_____.
+1,点P为边AB上一动点,过点P作PD⊥BC于点D,PE⊥AC于点E,则DE的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
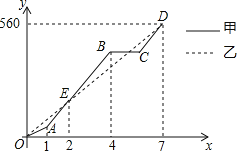
【题目】端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶,途中体息了一段时间后,仍按照每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程![]() ,
,![]() 与时间
与时间![]() 之间的函数关系的图象
之间的函数关系的图象![]() 请根据图象提供的信息,解决下列问题:
请根据图象提供的信息,解决下列问题:
![]() 图中E点的坐标是______,题中
图中E点的坐标是______,题中![]() ______
______![]() ,甲在途中休息______h;
,甲在途中休息______h;
![]() 求线段CD的解析式,并写出自变量x的取值范围;
求线段CD的解析式,并写出自变量x的取值范围;
![]() 两人第二次相遇后,又经过多长时间两人相距20km?
两人第二次相遇后,又经过多长时间两人相距20km?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com