
【题目】某教育主管部门针对中小学生非统考学科的教学情况进行年终考评,抽取某校八年级部分同学的成绩作为样本,把成绩按![]() (优秀)、
(优秀)、![]() (良好)、
(良好)、![]() (及格)、
(及格)、![]() (不及格)四个级别进行统计,并绘成如图所示不完整的条形统计图和扇形统计图.
(不及格)四个级别进行统计,并绘成如图所示不完整的条形统计图和扇形统计图.
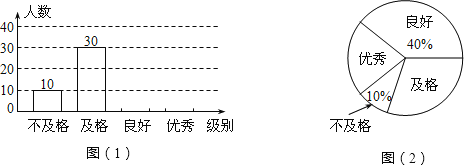
(1)求被抽取的学生人数;
(2)补全条形统计图,并求![]() 的圆心角度数;
的圆心角度数;
(3)该校八年级有![]() 名学生,请估计达到
名学生,请估计达到![]() 、
、![]() 两级的总人数.
两级的总人数.
科目:初中数学 来源: 题型:
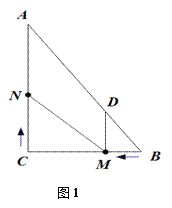
【题目】如图1,在Rt△ABC中,∠C=90,BC=6,AC=8.动点M从点B开始沿边BC向点C以每秒1个单位长度的速度运动,动点N从点C开始沿边CA向点A以每秒2个单位长度的速度运动,点M、N同时出发,且当其中一点到达端点时,另一点也随之停止运动.过点M作MD∥AC,交AB于点D,连接MN.设运动时间为t秒(t≥0).
(1)当t为何值时,四边形ADMN为平行四边形?
(2)是否存在t的值,使四边形ADMN为菱形?若存在,求出t的值;若不存在,说明理由.并探究只改变点N的速度(匀速运动),使四边形ADMN在某一时刻为菱形,求点N的速度;
(3)如图2,在整个运动过程中,求出线段MN中点P所经过的路径长.
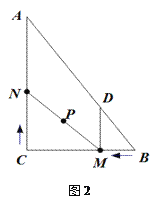
查看答案和解析>>
科目:初中数学 来源: 题型:
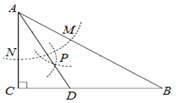
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上.
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦,
的弦,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
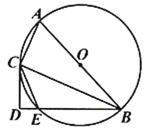
(1)![]() ________
________![]() (填“>”,“<”或“=”);
(填“>”,“<”或“=”);
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)若![]() 的直径为10,sin∠BAC=
的直径为10,sin∠BAC=![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今社会人们越来越离不开网络,电脑、手机被普遍使用,与此同时人们的视力也大大受到影响,2019年初某企业以25万元购得某项护目镜生产技术后,再投人100万元购买生产设备,进行该护目镜的生产加工,已知生产这种护目镜的成本价为每件20元,经过市场调研发现该产品的销售单价定在![]() 元比较合理,并且该产品的年销售量
元比较合理,并且该产品的年销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的函数关系式为
(元)之间的函数关系式为![]() .(年获利=年销售收入-生产成本-投资成本)
.(年获利=年销售收入-生产成本-投资成本)
(1)求该公司第一年的年获利![]() (万元)与销售单价
(万元)与销售单价![]() (元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?
(元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?
(2)2020年初我国爆发新冠肺炎,该公司决定向红十字会捐款20万元,另外每销售一件产品,就抽出1元钱作为捐款,若除去第一年的最大盈利(或最小亏损)以及第二年的捐款后,到2020年底,两年的总盈利不低于57.5万元,请你确定此时销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A′B′C′的位置,已知△ABC的面积为18,阴影部分三角形的面积为8,若AA′=1,则A′D的值为______.
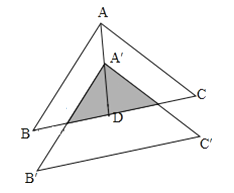
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把关于某一点成中心对称的两条抛物线叫“孪生抛物线”;(1)已知抛物线L:y=﹣x2+4与x轴交于A、B两点(A在B的左侧),与y轴交于C点,求L关于坐标原点O(0,0)的“孪生抛物线”W;(2)点N为坐标平面内一点,且△BCN是以BC为斜边的等腰直角三角形,在x轴是否存在一点M(m,0),使抛物线L关于点M的“孪生抛物线”过点N,如果存在,求出M点坐标;不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有![]() 两种型号的挖掘机,已知3台
两种型号的挖掘机,已知3台![]() 型和5台
型和5台![]() 型挖掘机同时施工一小时挖土165立方米;4台
型挖掘机同时施工一小时挖土165立方米;4台![]() 型和7台
型和7台![]() 型挖掘机同时施工一小时挖土225立方米.每台
型挖掘机同时施工一小时挖土225立方米.每台![]() 型挖掘机一小时的施工费用为300元,每台
型挖掘机一小时的施工费用为300元,每台![]() 型挖掘机一小时的施工费用为180元.
型挖掘机一小时的施工费用为180元.
(1)分别求每台![]() 型,
型, ![]() 型挖掘机一小时挖土多少立方米?
型挖掘机一小时挖土多少立方米?
(2)若不同数量的![]() 型和
型和![]() 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
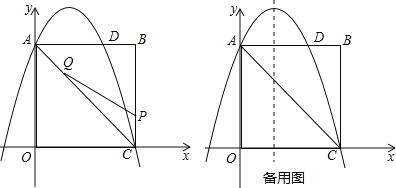
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com