
【题目】已知,如图,在边长为10的菱形ABCD中,cos∠B=![]() ,点E为BC边上的中点,点F为边AB边上一点,连接EF,过点B作EF的对称点B′,
,点E为BC边上的中点,点F为边AB边上一点,连接EF,过点B作EF的对称点B′,
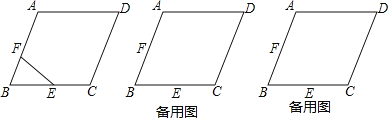
(1)在图(1)中,用无刻度的直尺和圆规作出点B′(不写作法,保留痕迹);
(2)当△EFB′为等腰三角形时,求折痕EF的长度.
(3)当B′落在AD边的中垂线上时,求BF的长度.
【答案】(1)尺规作图见解析;(2)EF=5或![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)分别以F、E为圆心,FB、EB为半径画弧,两弧交于点B,B即为所求;
(2)分情况①当BE=EF时,②BE=BF时,③EF=BF时讨论即可;
(3)连接BB,FE,可知BB⊥FE,依据翻折及勾股定理即可解得.
试题解析:(1)尺规作图:
(2)由翻折知:△FBE≌△FBE,
∴BE=BE,BF=BF,
∵点E为BC边上的中点,
∴BE=BE=5,
① 当BE=EF时,EF=5,
②当BE=BF时,过点F作FG⊥BE于点G,
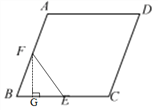
在Rt△FBG中,BE=BF=5,cos∠B=![]() ,
,
∴BG=![]() ,GE=BE-BG=
,GE=BE-BG=![]() ,
,
FG=![]() ,
,
在Rt△FEG中,FE=![]() ;
;
③当EF=BF时,
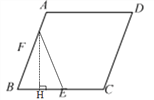
过点F作FH⊥BE于点H,BH=![]() BE=
BE=![]() ,
,
在Rt△FBH中, cos∠B=![]() ,
,
∴BF=BH×![]() =
=![]() ,
,
∴EF=![]() ,
,
综上:EF=5或![]() 或
或![]() .
.
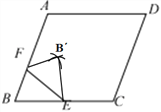
(3)
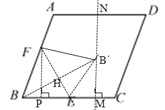
如图:连接BB,FE,交点 为H,
则BB⊥FE,
∵AN=DN=BE=CE=5,
∴EM=3,BE=BE=5,
∴BM=4,MN=![]() ,
,
BH=![]() ,
,
∴BF=BF=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2m+3)x+m2+2=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2,且满足x12+x22=31+|x1x2|,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了调动员工的积极性,决定实行目标管理,即确定个人年利润目标,根据目标完成的情况对员工进行适当的奖惩.为了确定这一目标,公司对上一年员工所创的年利润进行了抽样调查,并制成了如右的统计图.
(1)求样本容量,并补全条形统计图;
(2)求样本的众数,中位数和平均数;
(3)如果想让一半左右的员工都能达到目标,你认为个人年利润定为多少合适?如果想确定一个较高的目标,个人年利润又该怎样定才合适?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,五边形![]() 内部有若干个点,用这些点以及五边形
内部有若干个点,用这些点以及五边形![]() 的顶点
的顶点![]() 的顶点把原五边形分割成一些三角形(互相不重叠):
的顶点把原五边形分割成一些三角形(互相不重叠):

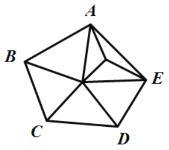
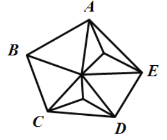
内部有1个点 内部有2个点 内部有3个点
(1)填写下表:
五边形 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 5 | 7 | 9 | … |
(2)原五边形能否被分割成2019个三角形?若能,求此时五边形![]() 内部有多少个点?若不能,请说明理由.
内部有多少个点?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
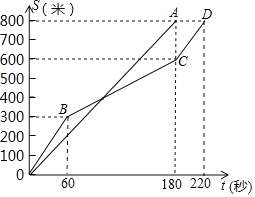
【题目】在女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数关系分別如图中线段OA和折线OBCD所示.
(1)谁先到终点,当她到终点时,另一位同学离终点多少米?(请直接写出答案)
(2)起跑后的60秒内谁领先?她在起跑后几秒时被追及?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
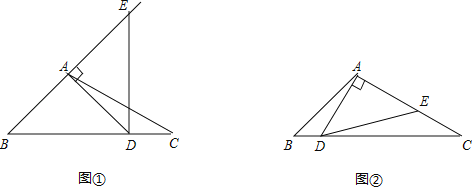
【题目】在△ABC中,∠B=45°,∠C=30°,点D是边BC上一点,连接AD,将线段AD绕点A逆时针旋转90°,得到线段AE,连接DE.
(1)如图①,当点E落在边BA的延长线上时,∠EDC= 度(直接填空);
(2)如图②,当点E落在边AC上时,求证:BD=![]() EC;
EC;
(3)当AB=2![]() ,且点E到AC的距离等于
,且点E到AC的距离等于![]() ﹣1时,直接写出tan∠CAE的值.
﹣1时,直接写出tan∠CAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设m,n是任意两个实数,规定m,n两数较大的的数称作这两个数的“绝对最值”,用sec(m,n)表示。例如:sec(-1,-2)=-1,sec(1,2)=2,sec(0,0)=0,参照上面的材料,解答下列问题:
(1)sec(![]() ,3.14)=________,sec(
,3.14)=________,sec(![]() ,
,![]() )=__________;
)=__________;
(2)若sec(-3x-1,x+1)=-3x-1,求x的取值范围;
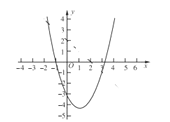
(3)求函数![]() 与
与![]() 的图象的交点坐标,函数
的图象的交点坐标,函数![]() 图象如图所示,请你在图中作出函数
图象如图所示,请你在图中作出函数![]() 的图象,并根据图象直接写出sec(-x+2,
的图象,并根据图象直接写出sec(-x+2, ![]() )的最小值。
)的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com