Question

【题目】如图,点在的边上,过点作的平行线,如果,那么的度数为__________．

Answer 1

【答案】（1）①中线；②是；（2）见解析；（3）.

【解析】

（1）①根据中线及二分线的定义即可求解；

②先由AD是BC边上的中线可得S△ABD=S△ACD，再根据可得S四边形ACFE=S△BEF即可求解；

（2）先证△CDG≌△EAG可得S△CDG=S△EAG，再根据F是EB的中点即可求解；

（3）分别证明△AEB≌△CDE，△AEB≌△EBH，△MHB≌△MAE，然后得出S△MHB=S△MAE，再根据全等三角形的性质及二分线定义即可求解．

（1）①三角形的中线、高线、角平分线中，一定是三角形的二分线的是中线，

故答案为中线；

②∵AD是BC边上的中线，

∴S△ABD=S△ACD,

又∵，

∴S四边形BEGD=S四边形AGFC，

∴S四边形BEGD+=S四边形AGFC+，

∴=S四边形AEFC，

所以EF是△ABC的一条二分线，故答案为是；

（2）∵点G是AD的中点，

∴GD=AG，

∵AB∥DC，

∴∠D=∠GAE，

在△CDG和△EAG中，

，

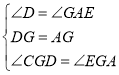∴△CDG≌△EAG（ASA），

∴S△CDG=S△EAG，

∵点F是EB的中点，

∴S△CFE=S△CBF，

即S△AGE+S四边形AGCF=S△CBF，

∴S△CDG+S四边形AGCF=S△CBF，即S四边形ADCF=S△CBF，

∴CF是四边形ABCD的二分线；

（3）如图，延长CB于点H，使得BH=AE，连接EH交AB于点M，

，

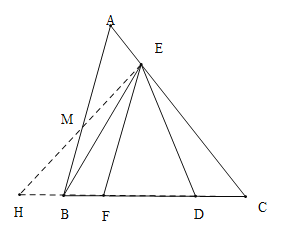∵AB=BC，

∴∠A=∠C，

∵∠BED＝∠A，

∴∠AEB＝∠CDE，

在△AEB和△CDE中，

，

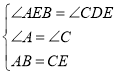∴△AEB≌△CDE（AAS），

∴AE=CD，

∴BH=CD，

∴DH=CB，

∵CB=CE，

∴∠CBE＝∠CEB，

∴∠HBE＝∠AEB，

在△EBH和△BEA中，

，

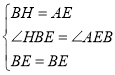∴△AEB≌△EBH（SAS），

∴∠H=∠A，

在△MBH和△MEA中，

，

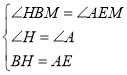∴△MHB≌△MAE（ASA），

∴S△MHB=S△MAE，

∴S△HMB+S四边形MBFE=S△AME+S四边形MBFE，即S△HEF=S四边形ABFE，

∵EF是四边形ABDE的一条二分线，

∴S四边形ABFE=S△DEF，

∴S△HEF=S△DEF，

∴DF=DH=CB=.