
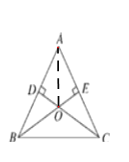
【题目】如图,锐角△ABC的两条高BE、CD相交于点O,且OB=OC,∠A=60°.
(1)求证:△ABC是等边三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.

【答案】(1)见解析;(2) 点O在∠BAC的平分线上,理由见解析.
【解析】
(1)由OB=OC,得∠OBC=∠OCB.再证∠BEC=∠CDB=90°由(AAS)可证△BCE≌△CBD,则∠DBC=∠ECB,所以,含有60°的等腰三角形是等边三角形;(2)由(1△BCE≌△CBD,得,EB=CD.又OB=OC,所以OE=OD,再由角平分线性质定理可证得.
(1)证明:∵OB=OC,∴∠OBC=∠OCB.
∵BE⊥AC,CD⊥AB,∴∠BEC=∠CDB=90°.
又∵BC=BC,∴△BCE≌△CBD(AAS),
∴∠DBC=∠ECB,∴AB=AC.
又∵∠A=60°,
∴△ABC是等边三角形.
(2)解:点O在∠BAC的平分线上.
理由如下:连接AO.由(1)可知△BCE≌△CBD,∴EB=CD.
∵OB=OC,∴OE=OD.
又∵OE⊥AC,OD⊥AB,
∴点O在∠BAC的平分线上.


科目:初中数学 来源: 题型:
【题目】甲骑自行车从A地出发,以每小时15km的速度驶向B地,经半小时后乙骑自行车从B地出发,以每小时20km的速度驶向A地,两人相遇时,乙已超过AB两地的中点5km,求A、B两地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乌苏市某生态示范园,计划种植一批苹果梨,原计划总产量达36万千克,为了满足市场需求,现决定改良苹果梨品种,改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万千克,种植亩数减少了20亩,则原计划和改良后平均每亩产量各多少万千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求值:1+2+22+23+24++22013.
解:设S=1+2+22+23+24+…+22013.将等式两边同时乘以2,得
2S=2+22+23+24+…+22013+22014
将下式减去上式,得2S﹣S=22014﹣1.
即S=1+2+22+23+24++22013=22014﹣1.
请你仿照此法计算1+3+32+33+34+…+32018的值是( )
A. 32018﹣1 B. ![]() C. 32019﹣1 D.
C. 32019﹣1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在300米环形跑道上练习长跑,甲的速度是6米/秒,乙的速度是7米/秒.
(1)如果甲、乙两人同地背向跑,乙先跑2秒,再经过多少秒两人相遇?
(2)如果甲、乙两人同地同向跑,乙跑几圈后能首次追上甲?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学每天中午总是在规定时间打开学校大门,七年级同学小明每天中午同一时间从家骑自行车到学校,星期一中午他以每小时15千米的速度到校,结果在校门口等了6分钟才开门,星期二中午他以每小时9千米的速度到校,结果校门已开了6分钟,星期三中午小明想准时到达学校门口,那么小明骑自行车的速度应该为每小时多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( ) 
A.102°
B.112°
C.115°
D.118°
查看答案和解析>>
科目:初中数学 来源: 题型:
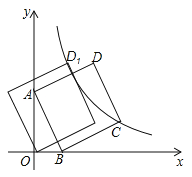
【题目】如图,直线![]() 与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线
与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线![]() (
(![]() )上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线
)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线![]() (
(![]() )上的点D1处,则a= .
)上的点D1处,则a= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C,B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.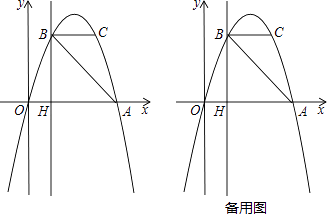
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当CM=MN,且∠CMN=90°时,求此时△CMN的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com