
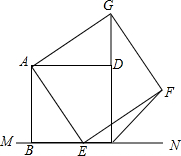
 如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.
如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.分析 (1)根据同角的余角相等得∠DAG=∠BAE,再根据“SAS”证得△ADG≌△ABE,即可得出DG的长;
(2)过F作BN的垂线,设垂足为H,首先证△ABE、△EHF全等,然后得AB=EH,BE=FH;然后根据AB=BC=EH,即BE+EC=EC+CH,得到CH=BE=FH,即可得证.
(3)在AB上取AQ=BE,连接QD,首先证△DAQ、△ABE、△ADG三个三角形全等,易证得AG、QD平行且相等,又由于AG、EF平行且相等,所以QD、EF平行且相等,即可得证.
解答 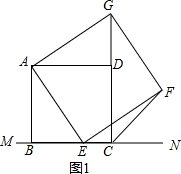 (1)解:如图1,连接DG
(1)解:如图1,连接DG
∵四边形ABCD和四边形AEFG是正方形,
∴DA=BA,EA=GA,∠BAD=∠EAG=90°,
∴∠DAG=∠BAE,
在△ADG和△ABE中,
∵$\left\{\begin{array}{l}{AD=AB}\\{∠DAG=∠BAE}\\{AG=AE}\end{array}\right.$,
∴△ADG≌△ABE(SAS),
∴BE=DG=1;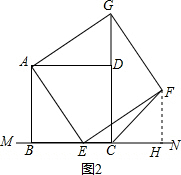
(2)证明:如图2,过F作BN的垂线,设垂足为H,
∵∠BAE+∠AEB=90°,∠FEH+∠AEB=90°,
∴∠BAE=∠HEF,
在△ABE和△EHF中
∵$\left\{\begin{array}{l}{∠EBA=∠EHF}\\{∠BAE=∠HEF}\\{AE=EF}\end{array}\right.$
∴△ABE≌△EHF(AAS),
∴AB=EH,BE=FH,
∴AB=BC=EH,
∴BE+EC=EC+CH,
∴CH=BE=FH,
∴∠FCN=45°;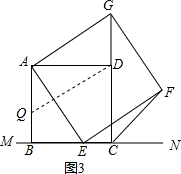
(3)解:如图3,在AB上取AQ=BE,连接QD,
在△DAQ和△ABE中,
∵$\left\{\begin{array}{l}{AD=AB}\\{∠DAQ=∠ABE}\\{AQ=BE}\end{array}\right.$,
∴△DAQ≌△ABE(SAS),
∵△ABE≌△EHF,
∴△DAQ≌△ABE≌△ADG,
∴∠GAD=∠ADQ,
∴AG、QD平行且相等,
又∵AG、EF平行且相等,∴QD、EF平行且相等,
∴四边形DQEF是平行四边形.
∴在AB边上存在一点Q,使得四边形DQEF是平行四边形.
点评 此题主要考查了全等三角形的判定与性质以及正方形的性质、平行四边形的判定等知识,熟练应用全等三角形的判定与性质是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
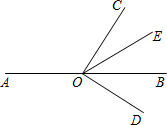 如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC.
如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 浙江卫视“奔跑吧兄弟”综艺节目的收视率,采用抽查的方式 | |
| B. | 了解某渔场中青鱼的平均重量,采用抽查的方式 | |
| C. | 了解iPhone6s手机的使用寿命,采用普查的方式 | |
| D. | 了解一批汽车的刹车性能,采用普查的方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
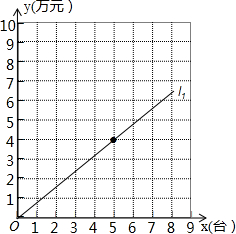 某专营商场销售一种品牌电脑,每台电脑的进货价是0.4万元.图中的直线l1表示该品牌电脑一天的销售收入y1(万元)与销售量x(台)的关系,已知商场每天的房租、水电、工资等固定支出为3万元.
某专营商场销售一种品牌电脑,每台电脑的进货价是0.4万元.图中的直线l1表示该品牌电脑一天的销售收入y1(万元)与销售量x(台)的关系,已知商场每天的房租、水电、工资等固定支出为3万元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
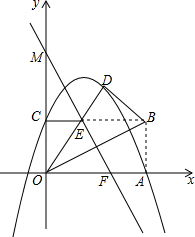 如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴和y轴的正半轴上,顶点B的坐标为(2m,m),沿着OB翻折△OAB,设翻折后的点A的应对点为点D,OD与BC交于点E,点M在y轴上,直线ME与x轴相交于点F,且∠EMC与∠MOB互余,经过点A,C,D的抛物线的解析式为y=ax2+bx+c.
如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴和y轴的正半轴上,顶点B的坐标为(2m,m),沿着OB翻折△OAB,设翻折后的点A的应对点为点D,OD与BC交于点E,点M在y轴上,直线ME与x轴相交于点F,且∠EMC与∠MOB互余,经过点A,C,D的抛物线的解析式为y=ax2+bx+c.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com