
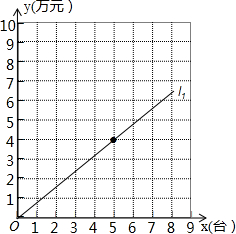
 某专营商场销售一种品牌电脑,每台电脑的进货价是0.4万元.图中的直线l1表示该品牌电脑一天的销售收入y1(万元)与销售量x(台)的关系,已知商场每天的房租、水电、工资等固定支出为3万元.
某专营商场销售一种品牌电脑,每台电脑的进货价是0.4万元.图中的直线l1表示该品牌电脑一天的销售收入y1(万元)与销售量x(台)的关系,已知商场每天的房租、水电、工资等固定支出为3万元.分析 (1)由函数图象知,y与x成正比例函数关系且过(5,4),待定系数法可求得直线l1对应的函数表达式,再根据每台电脑售价=每天销售收入÷销售量可得;
(2)根据:每天总成本=电脑的总成本+每天的固定支出,可列函数关系式;
(3)根据(2)中函数关系式,确定两点(0,3),(5,5),作射线即可;
(4)根据:商场每天利润=电脑的销售收入-每天的总成本,列出函数关系式,根据题意得到不等式、解不等式即可.
解答 解:(1)设y=kx,将(5,4)代入,得k=0.8,故y=0.8x,
每台电脑的售价为:$\frac{y}{x}=\frac{0.8x}{x}$=0.8(万元);
(2)根据题意,商场每天的总成本y2=0.4x+3;
(3)如图所示,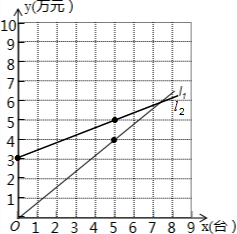
(3)商场每天的利润W=y-y2=0.8x-(0.4x+3)=0.4x-3,
当W>0,即0.4x-3>0时商场开始盈利,解得:x>7.5.
答:每天销售量达到8台时,商场可以盈利.
点评 本题主要考查一次函数的实际应用,熟悉一次函数解析式的求法、图象的画法及根据实际问题列函数关系式是一次函数的基础.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
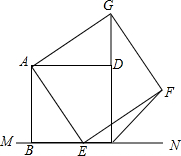 如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.
如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
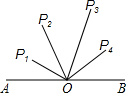 如图,O为线段AB的中点,AB=4cm,P1、P2、P3、P4到点O的距离分别是1cm、2cm、2.8cm、1.7cm,下列四点中能与A、B构成直角三角形的顶点是( )
如图,O为线段AB的中点,AB=4cm,P1、P2、P3、P4到点O的距离分别是1cm、2cm、2.8cm、1.7cm,下列四点中能与A、B构成直角三角形的顶点是( )| A. | P1 | B. | P2 | C. | P3 | D. | P4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C作⊙O的切线,交AB的延长线于点P.
如图,△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C作⊙O的切线,交AB的延长线于点P.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
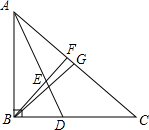 在△ABC中,∠ABC=90°,AD平分∠BAC,且BD=6,CD=9,在AD上取一点E使BE=BD,射线BE交AC于F,在线段FC上取一点G使GF:FA=1:8,连接BG,则线段BG的长为$\frac{9\sqrt{5}}{2}$.
在△ABC中,∠ABC=90°,AD平分∠BAC,且BD=6,CD=9,在AD上取一点E使BE=BD,射线BE交AC于F,在线段FC上取一点G使GF:FA=1:8,连接BG,则线段BG的长为$\frac{9\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com