
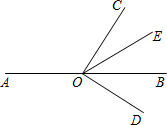
 如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC.
如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC.分析 (1)首先利用补角的定义可得出∠BOC,再利用角平分线的定义可得出∠COE,易得∠DOE;
(2)同理由(1)可得$∠DOE=\frac{1}{2}∠AOC$;
(3)设∠DOE=x,∠AOF=y,根据已知和(2)的结论可得出x-y=45°,从而得出结论.
解答 解:(1)若∠AOC=120°,
则∠BOC=180°-120°=60°,
∵OE平分∠BOC,
∴$∠COE=\frac{1}{2}∠BOC=\frac{1}{2}×60°=30°$,
∵∠COD=90°,
∴∠DOE=∠COD-∠COE=90°-30°=60°;
若∠AOC=140°,
则∠BOC=180°-140°=40°,
∵OE平分∠BOC,
∴$∠COE=\frac{1}{2}∠BOC=\frac{1}{2}×40°=20°$,
∵∠COD=90°,
∴∠DOE=∠COD-∠COE=90°-20°=70°;
故答案为:60°;70°;
(2)$\frac{1}{2}α$;
∵∠AOC=α,
∴∠BOC=180°-α,
∵OE平分∠BOC,
∴∠COE=$\frac{1}{2}∠BOC=90°-\frac{1}{2}α$,
∵∠COD=90°,
∴∠DOE=∠COD-∠COE=90°-(90$°-\frac{1}{2}α$)=$\frac{1}{2}α$,
故答案为:$\frac{1}{2}α$;
(3)∠DOE-∠AOF=45°.
理由:设∠DOE=x,∠AOF=y,
左边=∠AOC-3∠AOF=2∠DOE-3∠AOF=2x-3y,
右边=2∠BOE+∠AOF=2(90°-x)+y=180°-2 x+y,
∴2x-3y=180-2 x+y 即4x-4y=180°,
∴x-y=45°
∴∠DOE-∠AOF=45°.
点评 此题考查的知识点是角平分线的性质及角的计算,关键是正确运用好有关性质准确计算角的和差倍分.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| x | 1.0 | 1.1 | 1.2 | 1.3 |
| x2-8x+7.5 | 0.5 | -0.09 | -0.66 | -1.21 |
| A. | 1.0<x<1.1 | B. | 1.1<x<1.2 | C. | 1.2<x<1.3 | D. | 1.0<x<1.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
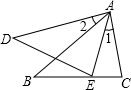 如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )| A. | ∠C=∠AED | B. | $\frac{AB}{AD}=\frac{AC}{AE}$ | C. | ∠B=∠D | D. | $\frac{AB}{AD}=\frac{BC}{DE}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ax2-a=a(x2-1) | B. | x2+x-2=x(x+1)-2 | C. | a2b+ab2=ab(a+b) | D. | x2+1=x(x+$\frac{1}{x}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
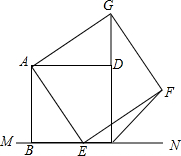 如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.
如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com