
【题目】如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D,点E在![]() 上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
(1)求证:CF⊥AB;
(2)若CD=4,CB=4![]() ,cos∠ACF=
,cos∠ACF=![]() ,求EF的长.
,求EF的长.

【答案】(1)详见解析;(2)2![]() .
.
【解析】试题分析:(1)连接BD,由AB是 O的直径,得到∠ADB=90°,根据余角的性质得到∠CFA=180°-(DAB+∠3)=90°,于是得到结论;
(2)连接OE,由∠ADB=90°,得到∠CDB=180°-∠ADB=90°,根据勾股定理得到DB=![]() =8解直角三角形得到CD=4,根据勾股定理即可得到结论.
=8解直角三角形得到CD=4,根据勾股定理即可得到结论.
试题解析:(1)连接BD,
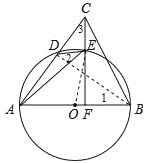
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠1=90°,
∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴∠DAB+∠3=90°,
∴∠CFA=180°﹣(DAB+∠3)=90°,
∴CF⊥AB;
(2)连接OE,
∵∠ADB=90°,
∴∠CDB=180°﹣∠ADB=90°,
∵在Rt△CDB中,CD=4,CB=4![]() ,
,
∴DB=![]() =8,
=8,
∵∠1=∠3,
∴cos∠1=cos∠3=![]() =
=![]() ,
,
∴AB=10,
∴OA=OE=5,AD=![]() =6,
=6,
∵CD=4,∴AC=AD+CD=10,
∵CF=ACcos∠3=8,
∴AF=![]() =6,
=6,
∴OF=AF﹣OA=1,
∴EF=![]() =2
=2![]() .
.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】问题情景:如图1,![]() 中,有一块直角三角板
中,有一块直角三角板![]() 放置在
放置在![]() 上(
上(![]() 点在
点在![]() 内),使三角板
内),使三角板![]() 的两条直角边
的两条直角边![]() 、
、![]() 恰好分别经过点
恰好分别经过点![]() 和点
和点![]() .
.
试问![]() 与
与![]() 是否存在某种确定的数量关系?
是否存在某种确定的数量关系?
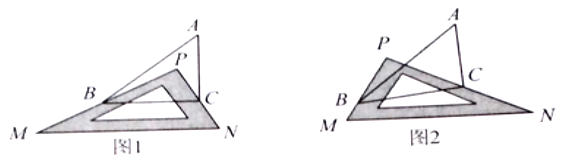
(1)特殊研究:若![]() ,则
,则![]() 度,
度,![]() 度,
度,![]() 度;
度;
(2)类比探索:请探究![]() 与
与![]() 的关系.
的关系.
(3)类比延伸:如图2,改变直角三角包![]() 的位置;使
的位置;使![]() 点在
点在![]() 外,三角板
外,三角板![]() 的两条直角边
的两条直角边![]() 、
、![]() 仍然分别经过点
仍然分别经过点![]() 和点
和点![]() ,(2)中的结论是否仍然成立?若不成立请直接写出你的结论.
,(2)中的结论是否仍然成立?若不成立请直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生课余生活,某区教育部分准备在七年级开设兴趣课堂,为了了解学生对音乐、书法、球类、绘画这四个兴趣小组的喜爱情况,在全区进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息不完整),请根据图中提供的信息,解答下面的问题:
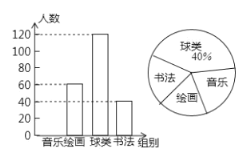
(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中音乐部分的圆心角的度数;
(3)如果该区七年级共有2000名学生参加这4个课外兴趣小组,则参加绘画兴趣小组的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
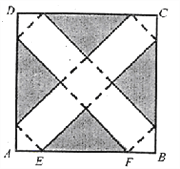
【题目】如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于底面上一点).已知E、F在AB边上,是被剪去一个等腰直角三角形斜边的两个端点,设AE=BF=xcm.
(1)若折成的包装盒恰好是正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顺次连结一四边形各边的中点,若所得的四边形是一个菱形,则原四边形一定是( ).
A.矩形B.对角线相互垂直的四边形
C.平行四边形D.对角线相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点 P 在平面直角坐标系中按图中箭头所示方向运动,第 1 次从原点运动到点(1,1),第 2 次接着运动到点(2,0),第 3 次接着运动到点(3,2),……,按这样的运动规律,经过第2025 次运动后,动点 P 的坐标是( )
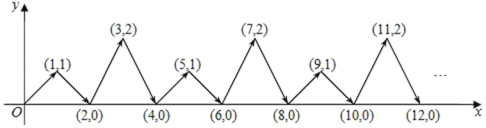
A.(2025,1)B.(2025,0)C.(2026,2)D.(2026,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com