
| 1 |
| 4 |


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
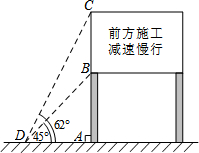 进入3月份,我市“两横三纵”快速路系统全线开工.为缓解市区内一些主要路段交通拥挤的现状,交警部门在一些主要路口设立了如图所示的交通路况显示牌.已知立杆AB的高度是3米,从地面上某处D点测得显示牌顶端C点和底端B点的仰角分别是62°和45°.求路况显示牌BC的高度.(精确到0.1米)
进入3月份,我市“两横三纵”快速路系统全线开工.为缓解市区内一些主要路段交通拥挤的现状,交警部门在一些主要路口设立了如图所示的交通路况显示牌.已知立杆AB的高度是3米,从地面上某处D点测得显示牌顶端C点和底端B点的仰角分别是62°和45°.求路况显示牌BC的高度.(精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:
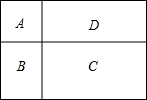 某农科站有一块长方形试验田,面积为1200m2.现要将其分为A、B、C、D四个区,其中A区为正方形.C区的长是30m,宽是20m.求A区的面积是多少平方米?
某农科站有一块长方形试验田,面积为1200m2.现要将其分为A、B、C、D四个区,其中A区为正方形.C区的长是30m,宽是20m.求A区的面积是多少平方米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com