
已知:▱ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.求证:BC=CF.


科目:初中数学 来源: 题型:
如图,正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1)连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题“在旋转的过程中,线段DF与BF的长始终相等”是否正确?若正确,请证明;若不正确,请举例说明;
(2)若将正方形AEFG绕点A按顺时针方向旋转,连接DG,在旋转过程中,你能否找到一条线段的长与线段DG的长始终相等?并以图为例说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
已知函数y=﹣x+4的图象与函数
 的图象在同一坐标系内.函数y=﹣x+4的图象如图1与坐标轴交于A、B两点,点M(2,m)是直线AB上一点,点N与点M关于y轴对称,线段MN交y轴于点C.
的图象在同一坐标系内.函数y=﹣x+4的图象如图1与坐标轴交于A、B两点,点M(2,m)是直线AB上一点,点N与点M关于y轴对称,线段MN交y轴于点C.
(1)m= ,S△AOB= ;
(2)如果线段MN被反比例函数
 的图象分成两部分,并且这两部分长度的比为1:3,求k的值;
的图象分成两部分,并且这两部分长度的比为1:3,求k的值;
(3)如图2,若反比例函数
 图象经过点N,此时反比例函数上存在两个点E(x1,y1)、F(x2,y2)关于原点对称且到直线MN的距离之比为1:3,若x1<x2请直接写出这两点的坐标.
图象经过点N,此时反比例函数上存在两个点E(x1,y1)、F(x2,y2)关于原点对称且到直线MN的距离之比为1:3,若x1<x2请直接写出这两点的坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于
 AB的长为半径画弧,两弧相交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
AB的长为半径画弧,两弧相交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )


A.矩形 B.菱形 C.正方形 D.等腰梯形
查看答案和解析>>
科目:初中数学 来源: 题型:
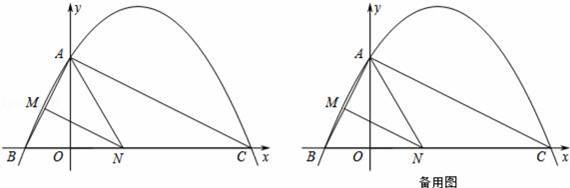
如图,已知二次函数y=ax2+
 x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+
 x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;
(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
阳光通过窗口AB照射到室内,在地面上留下2.7米的亮区DE(如图所示),已知亮区到窗口下的墙角的距离EC=8.7米,窗口高AB=1.8米,则窗口底边离地面的高BC为( )
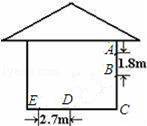

A.4米 B.3.8米 C.3.6米 D.3.4米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com